Integrale !
21 messages
- Page 1 sur 2 - 1, 2
Integrale !
Bonjour, Je vous propose un vrais défis de maths ,que je n'ai arrivé à le résoudre, Merci d'essayer de votre part et de proposer quelques solution, si vous en trouver quelques unes.
})
L'une de mes marottes, c'est d'inventer des exercices faisables en terminale d'après le programme, mais extrêmement difficiles... En voici un qui est très simple à faire avec les notions de bac+2 mais qui m'avait obligé à pas mal réfléchir pour me limiter aux notions du lycée.
Je suis parti d'un exercice trouvé sur des annales de bac où l'on étudiait la fonction x-->(ln x)². Je me suis demandé ce qui se passait avec (log x)^n. Je le donne sans indication (sinon ce n'est pas un défi...)
Pour tout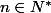 on définit la fonction
on définit la fonction  par
par  = \left\( \ln x \right\)^n) et on note
et on note  la courbe d'équation
la courbe d'équation ) .
.
a) Montrer que toute les courbes sont concourantes en exactement deux points A et B (on notera A celui de plus petite abscisse).
sont concourantes en exactement deux points A et B (on notera A celui de plus petite abscisse).
b) On note l'aire comprise entre l'axe des abscisses et
l'aire comprise entre l'axe des abscisses et  entre A et B (bref, c'est l'intégrale). Montrer que
entre A et B (bref, c'est l'intégrale). Montrer que  (résultat qui pourrait surprendre puisque
(résultat qui pourrait surprendre puisque  est non-nul en B).
est non-nul en B).
La difficulté de la question b) est qu'on n'a pas le droit d'intervertir la limite et la signe d'intégration puisque, en terminale, on ne connaît pas les critères pour le faire.
Edit : je viens de me rendre compte qu'il y a un forum pour les défis, zut. Cela dit mon message n'est pas vraiment un défi (je ne vous demande pas de le relever, je voulais juste partager avec vous cet énoncé), il est plus dans la continuité du message d'otmaneo qui parlait d'intégrale.
Je suis parti d'un exercice trouvé sur des annales de bac où l'on étudiait la fonction x-->(ln x)². Je me suis demandé ce qui se passait avec (log x)^n. Je le donne sans indication (sinon ce n'est pas un défi...)
Pour tout
a) Montrer que toute les courbes
b) On note
La difficulté de la question b) est qu'on n'a pas le droit d'intervertir la limite et la signe d'intégration puisque, en terminale, on ne connaît pas les critères pour le faire.
Edit : je viens de me rendre compte qu'il y a un forum pour les défis, zut. Cela dit mon message n'est pas vraiment un défi (je ne vous demande pas de le relever, je voulais juste partager avec vous cet énoncé), il est plus dans la continuité du message d'otmaneo qui parlait d'intégrale.
Robic a écrit:mon message n'est pas vraiment un défi (je ne vous demande pas de le relever, je voulais juste partager avec vous cet énoncé), il est plus dans la continuité du message d'otmaneo qui parlait d'intégrale.
Avec une intégration par parties, on trouve
Cela permet d'expliciter
Ca ne donne pas la limite.
A mon avis, d'avoir pris une fonction convexe (le log en l'occurrence), ça "tue" pas mal l'exo : tu le majore bêtement par la corde qui relie les deux extrémités et c'est fini vu qu'on intègre (ax+b)^n sans problèmes.Robic a écrit:b) On notel'aire comprise entre l'axe des abscisses et
entre A et B (bref, c'est l'intégrale). Montrer que
(résultat qui pourrait surprendre puisque
est non-nul en B).
ça serait un peu plus intéressant (à mon avis) avec une fonction concave...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
Perso, je ferais come ça :
\big)^2) est convexe (
est convexe ( ) donc la courbe de g est en dessous de la corde entre 1 et
) donc la courbe de g est en dessous de la corde entre 1 et  :
:
\big)^2\leq\frac{x-1}{e-1})
(Et cette inégalité peut se montrer sans connaitre la notion de convexité en dérivant la différence entre les deux membres)
Il s'ensuit que :
\big)^{2k}\,dx\leq \int_1^e\Big(\frac{x-1}{e-1}\Big)^k\,dx=\frac{1}{(e-1)^k}\int_0^{e-1} t^k\,dt<br />=\frac{1}{(e-1)^k}\frac{(e-1)^{k+1}}{k+1}=\frac{e-1}{k+1}\longrightarrow 0)
Et c'est suffisant vu que la suite_{n\geq 1}) est décroissante.
est décroissante.
Perso, je ferais come ça :
(Et cette inégalité peut se montrer sans connaitre la notion de convexité en dérivant la différence entre les deux membres)
Il s'ensuit que :
Et c'est suffisant vu que la suite
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Waou, c'est astucieux tout ça !
Ce que j'avais fait avait été guidé par le dessin : la courbe semble se plaquer contre l'axe des abscisses entre 1 et e, e non compris, et contre la droite {x = e} pour x=e. Du coup ça me suggérait de découper l'intégrale en deux : sur [1;u] et
sur [1;u] et 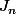 sur [u;e] où u est un certain nombre dans ]1;e[, et ensuite je compte majorer la fonction, j'écrirais alors que l'intégrale de la fonction est inférieure à l'intégrale du majorant. Par exemple :
sur [u;e] où u est un certain nombre dans ]1;e[, et ensuite je compte majorer la fonction, j'écrirais alors que l'intégrale de la fonction est inférieure à l'intégrale du majorant. Par exemple : dx = \int_1^u f_n(u)dx = (u-1)f_n(u)) qui tend vers 0 puisque
qui tend vers 0 puisque ) tend vers 0. Mais ça ne marche pas pour
tend vers 0. Mais ça ne marche pas pour 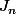 : le majorant est toujours 1.
: le majorant est toujours 1.
D'où l'idée de choisir, non pas u, mais de sorte que
de sorte que  tend vers e. Ainsi, l'intégrale de gauche tendra vers 0 parce que son majorant tend vers 0, et l'intégrale de droite tendra vers 0 parce que la largeur de l'intervalle d'intégration tend vers 0 (c'est en fait ça qui m'a été suggéré par le dessin, pas le fait de bêtement couper en deux). Encore faut-il trouver
tend vers e. Ainsi, l'intégrale de gauche tendra vers 0 parce que son majorant tend vers 0, et l'intégrale de droite tendra vers 0 parce que la largeur de l'intervalle d'intégration tend vers 0 (c'est en fait ça qui m'a été suggéré par le dessin, pas le fait de bêtement couper en deux). Encore faut-il trouver  qui tend vers e, mais pas trop vite afin que
qui tend vers e, mais pas trop vite afin que ) tende bien vers 0 (et non vers 1 par exemple). Et là ce n'est pas évident, d'autant qu'on ne peut pas calculer grand chose. Par exemple j'avais essayé
tende bien vers 0 (et non vers 1 par exemple). Et là ce n'est pas évident, d'autant qu'on ne peut pas calculer grand chose. Par exemple j'avais essayé 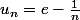 et je ne sais plus si c'était incalculable (probablement) ou si ça ne marchait pas.
et je ne sais plus si c'était incalculable (probablement) ou si ça ne marchait pas.
L'idée m'est venue en regardant le dessin où figurait la courbe à côté de la courbe
à côté de la courbe  : définir
: définir  comme étant la valeur qui maximise
comme étant la valeur qui maximise 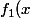-f_n(x)) entre 1 et e (l'endroit où la courbe
entre 1 et e (l'endroit où la courbe  s'écarte le plus de la courbe
s'écarte le plus de la courbe  ). Ainsi, je me doute que
). Ainsi, je me doute que ) va tendre vers 0 et non pas vers 1 (si ça tendait vers 1, la distance maxi entre les deux courbes tendrait vers 0, impossible d'après le dessin). De plus je vois bien, en faisant augmenter n, que
va tendre vers 0 et non pas vers 1 (si ça tendait vers 1, la distance maxi entre les deux courbes tendrait vers 0, impossible d'après le dessin). De plus je vois bien, en faisant augmenter n, que  augmente et s'approche de e. Reste juste à faire les calculs.
augmente et s'approche de e. Reste juste à faire les calculs.
En étudiant=f_1(x)-f_n(x)) on trouve un maximum pour
on trouve un maximum pour 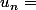 exp
exp^{1/(n-1)}\right\]) . On peut démontrer que ce nombre appartient bien à ]1;e[ et que sa limite est bien e. De plus :
. On peut démontrer que ce nombre appartient bien à ]1;e[ et que sa limite est bien e. De plus :  = \left\(\frac{1}{n}\right\)^{n/(n-1)}) qui tend bien vers 0. (Tous ces calculs de limite sont faisables en terminale : celle de
qui tend bien vers 0. (Tous ces calculs de limite sont faisables en terminale : celle de  nécessite de connaître la limite en 0 de
nécessite de connaître la limite en 0 de 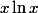 , qu'on voit en terminale, et la limite de
, qu'on voit en terminale, et la limite de ) n'est pas indéterminée.)
n'est pas indéterminée.)
Bref, on peut maintenant écrire :
-f_n(u_n)) qui tend vers 0 parce que
qui tend vers 0 parce que ) tend vers 0.
tend vers 0.
-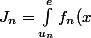dx) tend vers 0 parce que l'intervalle d'intégration tend à être de mesure nulle (tandis que la fonction est comprise entre 0 et 1).
tend vers 0 parce que l'intervalle d'intégration tend à être de mesure nulle (tandis que la fonction est comprise entre 0 et 1).
Ça fait nettement plus de calculs...
Ce que j'avais fait avait été guidé par le dessin : la courbe semble se plaquer contre l'axe des abscisses entre 1 et e, e non compris, et contre la droite {x = e} pour x=e. Du coup ça me suggérait de découper l'intégrale en deux :
D'où l'idée de choisir, non pas u, mais
L'idée m'est venue en regardant le dessin où figurait la courbe
En étudiant
Bref, on peut maintenant écrire :
-
-
Ça fait nettement plus de calculs...
Ta méthode est la bonne dans un cas trés général (on peut remplacer x->ln(x) par pas mal de truc : ça continue à marcher)
Alors que la mienne utilise une "faille" dans ton énoncé : la fonction en question (x->ln(x)) a une dérivée strictement positive au point x=e donc en l'élevant à une puissance suffisante, on peut rendre la dérivée en x=e aussi grande qu'on veut et finir par faire passer la courbe de la fonction à la puissance n en dessous de la corde, et là, c'est plié vu que la fonction (affine) de la corde, on sait parfaitement bien l'intégrer.
Pour rendre l'exo plus dur, il faut donc prendre une fonction f qui, à l'extrémité b où f(b)=1, vérifie en plus f'(b)=0. (et d'ailleurs, dans ce cas là, l'intégrale tend encore moins vite vers 0...)
Alors que la mienne utilise une "faille" dans ton énoncé : la fonction en question (x->ln(x)) a une dérivée strictement positive au point x=e donc en l'élevant à une puissance suffisante, on peut rendre la dérivée en x=e aussi grande qu'on veut et finir par faire passer la courbe de la fonction à la puissance n en dessous de la corde, et là, c'est plié vu que la fonction (affine) de la corde, on sait parfaitement bien l'intégrer.
Pour rendre l'exo plus dur, il faut donc prendre une fonction f qui, à l'extrémité b où f(b)=1, vérifie en plus f'(b)=0. (et d'ailleurs, dans ce cas là, l'intégrale tend encore moins vite vers 0...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Tiens, je rebondis sur le message de chan79 plus haut.
On trouve en effet, en intégrant par parties, que pour tout n entier naturel :
A_n) .
.
De plus il est facile de constater que la suite) est décroissante :
est décroissante :
^n (\ln x - 1) \, dx) .
.
Sur [1;e], le premier facteur est positif, par contre le second est négatif, donc on intègre une fonction négative : l'intégrale est négative. On en déduit la décroissance.
Ainsi,) est une suite décroissante, elle est de plus minorée par 0 (c'est l'intégrale d'une fonction positive) : elle converge. Notons L sa limite. Mais d'abord je vais ré-écrire la relation de récurrence :
est une suite décroissante, elle est de plus minorée par 0 (c'est l'intégrale d'une fonction positive) : elle converge. Notons L sa limite. Mais d'abord je vais ré-écrire la relation de récurrence :
A_n = e - A_{n+1})
Par ailleurs les ne peuvent pas être égaux à e. En effet, on a
ne peuvent pas être égaux à e. En effet, on a  et de plus la suite est décroissante, donc tous ses termes sont inférieurs à e-1 qui est < e. (Au passage, on en déduit aussi que L <= e - 1 donc L est différent de e.) On peut donc écrire :
et de plus la suite est décroissante, donc tous ses termes sont inférieurs à e-1 qui est < e. (Au passage, on en déduit aussi que L <= e - 1 donc L est différent de e.) On peut donc écrire :
 .
.
On peut passer à la limite (je ne pouvais pas le faire au début à cause du (n+1)An qui était indéterminé), en rappelant que L est différent de e :
 .
.
Il n'y a pas le choix : L = 0. C'est plus simple que ma première méthode ! Et puis c'est intéressant parce que ça mène à utiliser des suites, toujours au programme de terminale.
(La fin est bizarre, mais je ne pouvais pas remplacer directement L dans la relation de récurrence...)
-------
Je pense à un truc... Au début j'avais :
A_n = e - A_{n+1})
Si je passe à la limite dans le membre de droite, j'obtiens e - L, qui est un nombre réel constant (puisque L existe, donc est finie). Dans le membre de gauche, j'ai un truc du style l'infini fois L. Puisque l'infini fois L donne une constante, nécessairement L = 0. Non ?
Mieux : est-ce que ça ne prouve pas, du coup, que An est équivalent à e/(n+1) c'est-à-dire e/n ? En effet, (n+1)An tend vers e, donc An divisé par e/(n+1) tend vers 1. Sauf que je n'ai passé à la limite que dans le membre de droite, ce qui est bizarre... (Et de toute façon on sort du programme de terminale..)
On trouve en effet, en intégrant par parties, que pour tout n entier naturel :
De plus il est facile de constater que la suite
Sur [1;e], le premier facteur est positif, par contre le second est négatif, donc on intègre une fonction négative : l'intégrale est négative. On en déduit la décroissance.
Ainsi,
Par ailleurs les
On peut passer à la limite (je ne pouvais pas le faire au début à cause du (n+1)An qui était indéterminé), en rappelant que L est différent de e :
Il n'y a pas le choix : L = 0. C'est plus simple que ma première méthode ! Et puis c'est intéressant parce que ça mène à utiliser des suites, toujours au programme de terminale.
(La fin est bizarre, mais je ne pouvais pas remplacer directement L dans la relation de récurrence...)
-------
Je pense à un truc... Au début j'avais :
Si je passe à la limite dans le membre de droite, j'obtiens e - L, qui est un nombre réel constant (puisque L existe, donc est finie). Dans le membre de gauche, j'ai un truc du style l'infini fois L. Puisque l'infini fois L donne une constante, nécessairement L = 0. Non ?
Mieux : est-ce que ça ne prouve pas, du coup, que An est équivalent à e/(n+1) c'est-à-dire e/n ? En effet, (n+1)An tend vers e, donc An divisé par e/(n+1) tend vers 1. Sauf que je n'ai passé à la limite que dans le membre de droite, ce qui est bizarre... (Et de toute façon on sort du programme de terminale..)
Tout à fait mr_pyer, et cette preuve s'applique exactement de la même façon à n'importe quelle fonction strictement croissante de [a,b] dans [0,1].mr_pyer a écrit:Je fixe,
.
Ensuitelorsque
.
Ainsisi
est assez grand.
Sauf que vu la façon dont Robic procède dans son post du 25/03/2014 19h26, j'ai l'impression que la définition des limites avec des epsilon n'est plus du programme de terminale et qu'on a uniquement des "fonctions de références" auquel il faut se ramener : c'est pour ça qu'au lieu de prendre un simple epsilon fixé dans sa preuve, il est obligé de prendre un truc qui dépend de n de façon à avoir une majoration explicite de l'intégrale In par une quantité dépendant de n.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ah mais oui, c'est le contraire de l'autre ! Donc la difficulté est située dans la première intégrale, et on peut montrer effectivement que pour tout  , il existe un n à partir duquel l'intégrale entre 0 et 1 est inférieur à
, il existe un n à partir duquel l'intégrale entre 0 et 1 est inférieur à  . En terminale on ne voit plus la définition de la limite avec des
. En terminale on ne voit plus la définition de la limite avec des  , mais je pense qu'on doit pouvoir se raccrocher à la définition de terminale (« une suite admet une limite l lorsque tout intervalle ouvert centré en l contient tous les termes de la suite à partir d'un certain indice ») : mr_pyer a montré que tout ]-
, mais je pense qu'on doit pouvoir se raccrocher à la définition de terminale (« une suite admet une limite l lorsque tout intervalle ouvert centré en l contient tous les termes de la suite à partir d'un certain indice ») : mr_pyer a montré que tout ]- ;
; [ contient tous les termes de la suite à partir d'un certain indice (pour la deuxième intégrale il suffit d'expliquer que, puisqu'elle tend vers 0, l'intervalle ]-
[ contient tous les termes de la suite à partir d'un certain indice (pour la deuxième intégrale il suffit d'expliquer que, puisqu'elle tend vers 0, l'intervalle ]- ;
; [ contient tous les termes etc., donc elle est inférieure à
[ contient tous les termes etc., donc elle est inférieure à  ). Bon, ça va être laborieux quand même...
). Bon, ça va être laborieux quand même...
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
