Factorisation dans les racines
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
MattFellow
- Membre Naturel
- Messages: 31
- Enregistré le: 11 Nov 2013, 17:02
-
 par MattFellow » 23 Mar 2014, 13:48
par MattFellow » 23 Mar 2014, 13:48
Bonjours à tous,
en lisant la correction d'un exercice de Math je suis tombé sur la simplification suivante :

=
+sqrt{1/x^3}}})
Je me demandait si il existait un cours qui généraliserait les factorisation à l'intérieur des racines pour mieux comprendre comment l'utiliser dans tous les cas.
Merci de votre aide

-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 23 Mar 2014, 17:18
par Tiruxa » 23 Mar 2014, 17:18
D'abord il y a une erreur dans le résultat, ensuite il s'agit de mettre x en facteur sous la racine.
Se rappeler simplement que lorsque l'on met x en facteur dans une somme cela revient à diviser chaque terme de la somme par x.
autre remarque on utilise aussi

et

ainsi que les propriétés sur la racine carrée d'un produit ou d'un quotient.
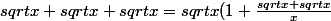} = sqrt{x(1+\frac{sqrt{x+sqrt{x}}}{\sqrt{x^2}})} =\sqrt{x}\sqrt{1+\sqrt{\frac{x+sqrt{x}}{x^2}}}<br />=\sqrt{x}\sqrt{1+\sqrt{\frac{1}{x}+\frac{sqrt{x}}{x^2}}}=\sqrt{x}\sqrt{1+\sqrt{\frac{1}{x}+\sqrt{ \frac{x}{x^4}}}}=\sqrt{x}\sqrt{1+\sqrt{\frac{1}{x}+\sqrt{ \frac{1}{x^3}}}})
-
MattFellow
- Membre Naturel
- Messages: 31
- Enregistré le: 11 Nov 2013, 17:02
-
 par MattFellow » 24 Mar 2014, 20:55
par MattFellow » 24 Mar 2014, 20:55
Merci Tiruxa,
je comprend mieux comment factoriser dans ce cas, il faut d'abord f
-
MattFellow
- Membre Naturel
- Messages: 31
- Enregistré le: 11 Nov 2013, 17:02
-
 par MattFellow » 24 Mar 2014, 20:56
par MattFellow » 24 Mar 2014, 20:56
* factoriser dans la racine puis traiter chaque sous racine une par une si j'ai bien compris :)
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 24 Mar 2014, 21:09
par Tiruxa » 24 Mar 2014, 21:09
Oui c'est bien comme cela que j'ai fait.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
