Bonsoir,
Je bloque à la dernière question de mon devoir maison que je dois rendre ce Lundi.
Je dois étudier les branches infinies en +infini de la fonction
f(x)=x²*ln((x+1)/(x-1))
en utilisant (ou pas ?) le développement limité.
Merci d'avance.
Développement limité et branches infinies
40 messages
- Page 1 sur 2 - 1, 2
par adrien69 » 22 Mar 2014, 21:52
Salut, si je te dis que (x+1)/(x-1) c'est en fait 1-2/(x-1), pour x>1, tu es capable avec un petit DL de me donner la limite de f(x)/x ?
par siger » 22 Mar 2014, 22:07
bonsoir
attention: faute de frappe!
(x+1)/(x-1) = (x +1 - 1 + 1)/( x-1) = ( x-1)/(x-1) + 2 /( x-1 ) = 1+ 2/(x-1)
.....
attention: faute de frappe!
(x+1)/(x-1) = (x +1 - 1 + 1)/( x-1) = ( x-1)/(x-1) + 2 /( x-1 ) = 1+ 2/(x-1)
.....
par Robic » 22 Mar 2014, 23:06
Un développement en 0 ? Pour trouver des branches infinies ??? :dingue2:
Ce qui pourrait être utile, c'est de trouver une développement du type f(x) = ax + b + o(1), mais en l'infini bien sûr. Un tel développement prouverait l'existence d'une asymptote oblique (et on peut connaître la position de la courbe grâce au terme suivant).
----
J'ajoute un truc... Je viens de faire le calcul, on trouve effectivement une asymptote oblique. Mais je n'ai pas eu besoin d'écrire :
 = \ln\left\( 1 + \frac{2}{x-1} \right\))
qui, à mon avis, conduit à des calculs plus compliqués (il faut poser
et espérer ne pas avoir besoin de y²...) que d'écrire :
 = \ln\left\(\frac{1+\frac{1}{x}}{1-\frac{1}{x}}\right\) = \ln\left\( 1+\frac{1}{x} \right\) - \ln\left\( 1-\frac{1}{x} \right\))
(en divisant tout le monde par x) afin de faire apparaître le changement de variable y=1/x qui est quand même plus simple. On pourra ensuite développer ln(1+y) et ln(1-y).
----
Au fait : comment savoir jusqu'à quel ordre on va développer ?
--> Il y a une stratégie, on ne le choisit pas au hasard.
On va poser y=1/x et on va développer les logarithmes, donc a priori la différence des logarithmes admettra un développement du type a + by + cy² + dy^3 + ... (je n'indique pas où on s'arrête). Ensuite on divise par y² (puisqu'on multiplie par x² et que x=1/y) donc le développement de f sera a/y² + b/y + c + dy + ... qui est égal à ax² + bx + c + d/x + ...
- S'il y a une branche parabolique, le premier terme suffisait.
- S'il y a une asymptote oblique, a est nul et y=bx+c est l'équation de cette droite, donc il faut le coefficient c.
Comme on ne sait pas à l'avance, on est obligé de développer jusqu'au coefficient c, donc on doit faire un développement limité des logarithmes qui contient a + by + cy², donc d'ordre 2.
(Si on veut connaître la position de la courbe par rapport à l'asymptote, il faut développer jusqu'au prochain coefficient non nul, et là on ne peut pas deviner lequel c'est à l'avance. Dans ce cas on essaie un degré de plus en espérant que le coefficient en question n'est pas nul.)
Ce qui pourrait être utile, c'est de trouver une développement du type f(x) = ax + b + o(1), mais en l'infini bien sûr. Un tel développement prouverait l'existence d'une asymptote oblique (et on peut connaître la position de la courbe grâce au terme suivant).
----
J'ajoute un truc... Je viens de faire le calcul, on trouve effectivement une asymptote oblique. Mais je n'ai pas eu besoin d'écrire :
qui, à mon avis, conduit à des calculs plus compliqués (il faut poser
(en divisant tout le monde par x) afin de faire apparaître le changement de variable y=1/x qui est quand même plus simple. On pourra ensuite développer ln(1+y) et ln(1-y).
----
Au fait : comment savoir jusqu'à quel ordre on va développer ?
--> Il y a une stratégie, on ne le choisit pas au hasard.
On va poser y=1/x et on va développer les logarithmes, donc a priori la différence des logarithmes admettra un développement du type a + by + cy² + dy^3 + ... (je n'indique pas où on s'arrête). Ensuite on divise par y² (puisqu'on multiplie par x² et que x=1/y) donc le développement de f sera a/y² + b/y + c + dy + ... qui est égal à ax² + bx + c + d/x + ...
- S'il y a une branche parabolique, le premier terme suffisait.
- S'il y a une asymptote oblique, a est nul et y=bx+c est l'équation de cette droite, donc il faut le coefficient c.
Comme on ne sait pas à l'avance, on est obligé de développer jusqu'au coefficient c, donc on doit faire un développement limité des logarithmes qui contient a + by + cy², donc d'ordre 2.
(Si on veut connaître la position de la courbe par rapport à l'asymptote, il faut développer jusqu'au prochain coefficient non nul, et là on ne peut pas deviner lequel c'est à l'avance. Dans ce cas on essaie un degré de plus en espérant que le coefficient en question n'est pas nul.)
par mrif » 23 Mar 2014, 02:07
Matiut a écrit:Ah d'accord, maintenant je dois faire le DL de ln(1+2/(x-1) ?
Je reprends l'idée d'adrien69:
ln(1+2/(x-1)) est équivalent à 2/(x-1) en +l'infini
x²*ln(1+2/(x-1)) est équivalent à 2x²/(x-1) = [2(x²-1) + 2]/(x-1) = 2x+2 + 2/(x-1) en +l'infini, ce qui met en évidence l'asymptote oblique d'équation y = 2x + 2 en +l'infini.
par adrien69 » 23 Mar 2014, 02:13
mrif a écrit:Je reprends l'idée d'adrien69:
ln(1+2/(x-1)) est équivalent à 2/(x-1) en +l'infini
x²*ln(1+2/(x-1)) est équivalent à 2x²/(x-1) = [2(x²-1) + 2]/(x-1) = 2x+2 + 2/(x-1) en +l'infini, ce qui met en évidence l'asymptote oblique d'équation y = 2x + 2 en +l'infini.
Hello !
Attention à ton "est équivalent", parce que si on part là-dedans,
2x+2+2/(x-1) est équivalent à 2x à l'infini. Et donc quoi, l'asymptote oblique serait 2x ? Que nenni. C'est bien pour ça que les o() sont importants. Ton calcul est juste, mais mal justifié. Ou bien on traîne un o() tout du long, ou bien on y va étape par étape : f(x)/x tend vers 2, donc on va étudier la limite de f(x)-2x, si on trouve un réel b, alors on a une branche asymptotique donc l'équation sera 2x+b.
C'est aussi simple que ça.
par mrif » 23 Mar 2014, 02:26
adrien69 a écrit:Hello !
Attention à ton "est équivalent", parce que si on part là-dedans,
2x+2+2/(x-1) est équivalent à 2x à l'infini. Et donc quoi, l'asymptote oblique serait 2x ? Que nenni. C'est bien pour ça que les o() sont importants. Ton calcul est juste, mais mal justifié. Ou bien on traîne un o() tout du long, ou bien on y va étape par étape : f(x)/x tend vers 2, donc on va étudier la limite de f(x)-2x, si on trouve un réel b, alors on a une branche asymptotique donc l'équation sera 2x+b.
C'est aussi simple que ça.
Je n'ai pas compris ta remarque. Pourquoi 2x+2+2/(x-1) serait équivalent à 2x en +l'infini?
par Robic » 23 Mar 2014, 03:01
mrif : je reprends ton idéé, mais avec un développement limité :
 = \ln (1+y) = y + o(y) = \frac{2}{x-1} + o(\frac{1}{x}))
, où l'on a posé 
.
Du coup :
 = \frac{2x^2}{x-1} + o(x))
,
où)
, et donc :
 = 2x + o(x))
.
Mais ce développement limité ne va pas assez loin pour avoir la constante puisqu'il s'arrête à o(x), on ne peut donc pas avoir l'équation de l'asymptote oblique. Ici, on ne peut pas utiliser le fait que)
car depuis le début on fait un développement limité en o(x), pas en o(1). Pour le faire en o(1) on aurait dû calculer le terme suivant. (C'est bien sûr le même problème si on utilise un équivalent, qui est une sorte de développement limité avec un seul terme.)
Tout ce qu'on peut dire, c'est que s'il y a une asymptote, elle est d'équation y = 2x + b : c'est ce qu'adrien69 a expliqué plus haut.
Pour avoir la constante, il faut faire :
 = \ln (1+y) = y - \frac{y^2}{2}+ o(y^2) = \frac{2}{x-1} - \frac{1}{2}\left\( \frac{2}{x-1} \right\)^2 + o(\frac{1}{x^2}) = \frac{2}{x-1} - \frac{2}{(x-1)^2} + o(\frac{1}{x^2}))
.
Ainsi :
 = \frac{2x^2}{x-1} - \frac{2x^2}{(x-1)^2} + o(1))
.
Reste à développer les fractions :
)
^2} = 2 + \frac{4x-2}{(x-1)^2} = 2 + o(1))
Du coup ça donne :
 = 2x + 2 - 2 + o(1) = 2x + o(1))
.
L'asymptote oblique est donc la droite d'équation y = 2x. (Et non pas y = 2x + 2 : avec l'équivalent on loupe le -2 du deuxième terme. On peut faire la vérification à la calculatrice : f(x)-2x, pour des valeurs de l'ordre de 1000 ou 10000, s'approche de 0, pas de 2.)
C'est exactement ce que j'avais trouvé avec la méthode que j'ai exposée plus haut et qui est largement, mais alors largement plus simple (mais vraiment !). On peut même très facilement connaître la position de la courbe par rapport à l'asymptote en allant un degré plus loin (ça donne=2x + \frac{2}{3x} + o(\frac{1}{x}))
(et la calculatrice confirme : f(100)-200 ~ 0,00666, f(1000)-2000 ~ 0,000666, f(10000) - 20000 ~ 0,0000666, etc.)
Matiut : fais comme j'ai dit dans mon premier message ! Pas comme dans ce message ci...
Du coup :
où
Mais ce développement limité ne va pas assez loin pour avoir la constante puisqu'il s'arrête à o(x), on ne peut donc pas avoir l'équation de l'asymptote oblique. Ici, on ne peut pas utiliser le fait que
Tout ce qu'on peut dire, c'est que s'il y a une asymptote, elle est d'équation y = 2x + b : c'est ce qu'adrien69 a expliqué plus haut.
Pour avoir la constante, il faut faire :
Ainsi :
Reste à développer les fractions :
Du coup ça donne :
L'asymptote oblique est donc la droite d'équation y = 2x. (Et non pas y = 2x + 2 : avec l'équivalent on loupe le -2 du deuxième terme. On peut faire la vérification à la calculatrice : f(x)-2x, pour des valeurs de l'ordre de 1000 ou 10000, s'approche de 0, pas de 2.)
C'est exactement ce que j'avais trouvé avec la méthode que j'ai exposée plus haut et qui est largement, mais alors largement plus simple (mais vraiment !). On peut même très facilement connaître la position de la courbe par rapport à l'asymptote en allant un degré plus loin (ça donne
Matiut : fais comme j'ai dit dans mon premier message ! Pas comme dans ce message ci...
par mrif » 23 Mar 2014, 03:23
Robic a écrit:mrif : je reprends ton idéé, mais avec un développement limité :
Du coup :,
où, et donc :
.
Mais ce développement limité ne va pas assez loin pour avoir la constante puisqu'il s'arrête à o(x), on ne peut donc pas avoir l'équation de l'asymptote oblique.
Pour avoir la constante, il faut faire :.
Il y a quelques erreurs dans ta réponse:
Quand tu as écris:
Dans ce que j'ai écrit dans mon post précédent j'ai donné la valeur exacte du o(x) qui n'est autre que
par Robic » 23 Mar 2014, 03:26
J'ai corrigé une ou deux fautes de frappe, mais l'erreur que tu signales n'en est pas une :
 = o(x))
. Une constante n'est pas un o(x) ?
Je viens de vérifier la définition (tu m'as mis le doute) : y = o(x) si y/x tend vers 0. Une constante divisée par x (au voisinage de l'infini) tend bien vers 0, donc est un o(x).
De toute façon je suis à peu près sûr que tout ce que j'ai dit est essentiellement juste aux fautes de frappe près (ça a été confirmé par la calculatrice !) Donc :
(1) La bonne méthode, c'est le changement de variable tout simple y=1/x.
(2) La fonction admet comme asymptote y = 2x (et le terme suivant du développement est 2/(3x)).
(3) Utiliser un équivalent ne permet pas d'avoir l'équation de l'asymptote, juste le 2x (comme Adrien69 l'avait dit) et j'ai essayé de détailler pourquoi (il manque le -2 du terme suivant).
Je viens de vérifier la définition (tu m'as mis le doute) : y = o(x) si y/x tend vers 0. Une constante divisée par x (au voisinage de l'infini) tend bien vers 0, donc est un o(x).
De toute façon je suis à peu près sûr que tout ce que j'ai dit est essentiellement juste aux fautes de frappe près (ça a été confirmé par la calculatrice !) Donc :
(1) La bonne méthode, c'est le changement de variable tout simple y=1/x.
(2) La fonction admet comme asymptote y = 2x (et le terme suivant du développement est 2/(3x)).
(3) Utiliser un équivalent ne permet pas d'avoir l'équation de l'asymptote, juste le 2x (comme Adrien69 l'avait dit) et j'ai essayé de détailler pourquoi (il manque le -2 du terme suivant).
par mrif » 23 Mar 2014, 03:54
Robic a écrit:J'ai corrigé une ou deux fautes de frappe, mais l'erreur que tu signales n'en est pas une :
Je viens de vérifier la définition (tu m'as mis le doute) : y = o(x) si y/x tend vers 0. Une constante divisée par x (au voisinage de l'infini) tend bien vers 0, donc est un o(x).
De toute façon je suis à peu près sûr que tout ce que j'ai dit est essentiellement juste aux fautes de frappe près (ça a été confirmé par la calculatrice !) Donc :
(1) La bonne méthode, c'est le changement de variable tout simple y=1/x.
(2) La fonction admet comme asymptote y = 2x (et le terme suivant du développement est 2/(3x)).
(3) Utiliser un équivalent ne permet pas d'avoir l'équation de l'asymptote, juste le "2x" (comme Adrien l'avait dit) et j'ai essayé de détailler pourquoi (il manque le -2 du terme suivant).
Effectivement je viens de vérifier que l'asymptote est la droite d'équation y = 2x en utilisant le site http://www.wolframalpha.com/, mais je n'arrive pas à voir mon erreur.
Merci d'avoir insister pour corriger l'erreur.
Bonne nuit.
par Robic » 23 Mar 2014, 03:58
Voici deux points qui expliquent ton erreur :
- Tu utilises un équivalent qui est en fait un développement limité du logarithme à l'ordre 1 en y. Du coup le développement limité de f s'arrête à o(x), pas à o(1). Quand tu dis que la fraction je-sais-plus-quoi est égale à 2x + 2 + o(1), ça ne va pas, puisque ton développement s'arrête à o(x). Donc il faut utiliser 2x + o(x). Tu n'as pas le droit d'aller plus loin. Si tu veux utiliser la constante, il faut développer un ordre de plus (ce que j'ai fait), et on s'aperçoit alors que le terme suivant contient un -2, qui s'annule avec le +2 du premier terme.
- Un équivalent ne donne pas l'équation d'une asymptote oblique. Exemple : f(x) = x + 1 + 1/x est équivalent au voisinage de l'infini à g(x) = x puisque f/g tend vers 1. Pourtant son asymptote oblique est y = x + 1, pas y = x.
Dans cet exercice il y a deux méthodes et le calcul de l'équivalent est utile, mais pas suffisant :
- On démontre que f(x)~2x, donc que f(x)/(2x) tend vers 1, ce qui prouve qu'il existe une asymptote oblique d'équation y = 2x + b où b reste à déterminer (voir explications d'Adrien69).
- On écrit un développement limité au voisinage de l'infini qui commence par ax²+bx+c. Je trouve que c'est beaucoup plus rapide.
- Tu utilises un équivalent qui est en fait un développement limité du logarithme à l'ordre 1 en y. Du coup le développement limité de f s'arrête à o(x), pas à o(1). Quand tu dis que la fraction je-sais-plus-quoi est égale à 2x + 2 + o(1), ça ne va pas, puisque ton développement s'arrête à o(x). Donc il faut utiliser 2x + o(x). Tu n'as pas le droit d'aller plus loin. Si tu veux utiliser la constante, il faut développer un ordre de plus (ce que j'ai fait), et on s'aperçoit alors que le terme suivant contient un -2, qui s'annule avec le +2 du premier terme.
- Un équivalent ne donne pas l'équation d'une asymptote oblique. Exemple : f(x) = x + 1 + 1/x est équivalent au voisinage de l'infini à g(x) = x puisque f/g tend vers 1. Pourtant son asymptote oblique est y = x + 1, pas y = x.
Dans cet exercice il y a deux méthodes et le calcul de l'équivalent est utile, mais pas suffisant :
- On démontre que f(x)~2x, donc que f(x)/(2x) tend vers 1, ce qui prouve qu'il existe une asymptote oblique d'équation y = 2x + b où b reste à déterminer (voir explications d'Adrien69).
- On écrit un développement limité au voisinage de l'infini qui commence par ax²+bx+c. Je trouve que c'est beaucoup plus rapide.
par Matiut » 23 Mar 2014, 10:20
Bonjour à tous,
Je suis heureux de voir que mon exercice passionne. ^^
Au final je vais utiliser la méthode du développement limité, c'est-à-dire le post posté par Robic. Auparavant, je n'avais jamais fais de DL au voisinage de l'infini...
Je vais essayer de comprendre comment Robic a fait tout cela.
Je suis heureux de voir que mon exercice passionne. ^^
Au final je vais utiliser la méthode du développement limité, c'est-à-dire le post posté par Robic. Auparavant, je n'avais jamais fais de DL au voisinage de l'infini...
Je vais essayer de comprendre comment Robic a fait tout cela.
par Matiut » 23 Mar 2014, 10:29
La méthode la plus simple est donc de faire un DL d'ordre 2 de ln(1+1/x)-ln(1-1/x) ?
par Ben314 » 23 Mar 2014, 11:26
Salut,
Juste quelques remarques personelles dans le désordre (donc ça n'implique... que moi...) :
1) La plupart des auteurs (mais évidement pas tous...) parlent plutôt de dévelopement asymptotique et pas de développement limités lorsque x->oo ou bien lorsque le fameux D.L. contient des termes en x^négatif (en résumé, dés qu'il y a des trucs qui tendent vers l'infini dans le bidule)
2) A mon avis, pour ne pas s'emméler les pinceaux, dans le cas où x->oo, avant même de commencer à réfléchir, tu pose y=1/x de façon à avoir y->0 ce qui est plus "usuel" : les "formules classiques" de D.L. sont toutes données avec la variable qui tend vers 0 (de même, lorsque x->xo, avant de commencer à réfléchir, je pose y=x-xo de façon à avoir y->0)
3) Dans le cadre de cet exercice en particulier, je trouve que de poser y=1/x dés le départ comme l'a fait Robic ou de prendre y=2/(x+1) comme l'a fait adrien, c'est sur le principe assez semblable : on a ramené le truc à un y qui tend vers 0. Dans le premier cas y=1/x, c'est nettement moins chiant pour retrouver les x vu que y^{-n}=x^n alors que dans le second y^{-n}=((x+1)/2)^n et il faut développer.
4) Une fois qu'on a vu les D.L., je trouve que c'est un peu concon de chercher les assymptotes à coup de "a=lim f(x)/x" puis de "b=lim f(x)-ax" vu que justement les D.L. permettent de faire les deux en même temps (ils sont plus précis qu'une simple équivalence)
Juste quelques remarques personelles dans le désordre (donc ça n'implique... que moi...) :
1) La plupart des auteurs (mais évidement pas tous...) parlent plutôt de dévelopement asymptotique et pas de développement limités lorsque x->oo ou bien lorsque le fameux D.L. contient des termes en x^négatif (en résumé, dés qu'il y a des trucs qui tendent vers l'infini dans le bidule)
2) A mon avis, pour ne pas s'emméler les pinceaux, dans le cas où x->oo, avant même de commencer à réfléchir, tu pose y=1/x de façon à avoir y->0 ce qui est plus "usuel" : les "formules classiques" de D.L. sont toutes données avec la variable qui tend vers 0 (de même, lorsque x->xo, avant de commencer à réfléchir, je pose y=x-xo de façon à avoir y->0)
3) Dans le cadre de cet exercice en particulier, je trouve que de poser y=1/x dés le départ comme l'a fait Robic ou de prendre y=2/(x+1) comme l'a fait adrien, c'est sur le principe assez semblable : on a ramené le truc à un y qui tend vers 0. Dans le premier cas y=1/x, c'est nettement moins chiant pour retrouver les x vu que y^{-n}=x^n alors que dans le second y^{-n}=((x+1)/2)^n et il faut développer.
4) Une fois qu'on a vu les D.L., je trouve que c'est un peu concon de chercher les assymptotes à coup de "a=lim f(x)/x" puis de "b=lim f(x)-ax" vu que justement les D.L. permettent de faire les deux en même temps (ils sont plus précis qu'une simple équivalence)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Matiut » 23 Mar 2014, 11:31
Pourquoi Robic met au début o(1/x²) alors qu'il a posé y=2/x-1 ?
Et ensuite il change et il met o(1) ?
Je n'ai pas compris ça..
Et ensuite il change et il met o(1) ?
Je n'ai pas compris ça..
par Ben314 » 23 Mar 2014, 12:17
Si tu parle de ça :
Il ne faut JAMAIS, JAMAIS, JAMAIS, perdre de vu la définition d'un "petit o" :
truc=o(bidule) signifie que truc=bidule x qq_chose_qui_tend_vers_0 (lorsque la variable tend vers ...)
Si c'est pas ARCHI CLAIR dans ta tête, je te suggére fortement une autre notation, c'est à dire bidule x epsilon(bidule) à la place de o(bidule) pour bien COMPRENDRE ce que tu écrit.
Par exemple, ici,=y^2\varepsilon(y))
où \rightarrow 0)
lorsque y->0.
Donc=\Big(\frac{2}{x-1}\Big)^2\varepsilon\Big(\frac{2}{x-1}\Big)=\frac{1}{x^2}\varepsilon'(x))
avec =\frac{4x^2}{(x-1)^2}\varepsilon\Big(\frac{2}{x-1}\Big))
qui tend vers 0 lorsque x->oo vu que le morceau avant le 
tend vers 4 et le )
tend vers 0.
Conclusion :=o\Big(\frac{1}{x^2}\Big))
(mais c'est pas forcément super malin comme notation vu qu'il évidement comprendre que le premier "petit o" est "en 0" alors que le deuxième est "en +oo".
Concernant la 2em ligne, c'est encore plus con : un)
, c'est un )
où \rightarrow 0)
lorsque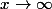 
.
Si tu multiplie par
, ben ça fait...
Robic a écrit:
Ainsi :
Il ne faut JAMAIS, JAMAIS, JAMAIS, perdre de vu la définition d'un "petit o" :
truc=o(bidule) signifie que truc=bidule x qq_chose_qui_tend_vers_0 (lorsque la variable tend vers ...)
Si c'est pas ARCHI CLAIR dans ta tête, je te suggére fortement une autre notation, c'est à dire bidule x epsilon(bidule) à la place de o(bidule) pour bien COMPRENDRE ce que tu écrit.
Par exemple, ici,
Donc
Conclusion :
Concernant la 2em ligne, c'est encore plus con : un
Si tu multiplie par
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
40 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :