Dérivées, différentielles et intégrales

[Anonyme]

Je suis en terminale S et je voulais mieux comprendre les notions de dérivés et d'intégrale, j'ai cherché un peu des exemples d'applications pour la physique et j'ai été très surpris

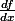
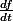
On m'a toujours appris que la dérivée notée était une entité mathématiques globale et non pas un rapport. Et j'ai été étonné lorsque j'ai vu comment on formait la dérivée particulaire par exemple : la différentielle totale exacte divisée par dt. Et on obtenait donc un rapport : mais je me demandais si c'était vraiment une dérivée, ou simplement on l'appelait somme ça parce que ça ressemblait à une dérivée ?

Ça m'a surpris qu'on puisse former des dérivés de manière '' libre'' alors que je croyais que c'était une autre écriture pour f'(x) et donc une entité mathématique globale.

Plus mystérieux encore, on m'a toujours appris qu'une intégrale avait toujours la forme de : En regardant un peu des exemples de mécanique j'ai remarqué qu'on pouvait former des intégrales beaucoup plus librement. J'ai en particulier lu un développement qui parler de prendre des infimes variations de quantités notées dx, dt, dz, ect. 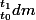Et qu'ensuite on '' intégrait '' l'équation et on se retrouver avec des entités du type : (où est la fonction ?) et j'ai vu que c'était des intégrales indefinies (sans bornes donc) qui je croyais designaient la primitive de la fonction après le '' sum'' et des intégrales définies (donc avec des bornes).

Donc c'est un peu confus :mur: . J'ai l'impression que ces notions sont beaucoup plus flexibles mais en même temps je ne sais pas si c'est propre à la physique...

Merci d'éclairer ma lanterne ! :zen:

[chan79]

si f(x)=x²+x
=2
f'(x)=2x+1
f'(2)=5

(0.01)=0.05
On peut estimer la variation de f à 0.05
En fait f(2.01)=6.0501 et l'estimation donne 6,05

[chan79]

Salut
La dérivée est la limite du taux de variation.
La différentielle de f en est l'application linéaire qui multiplie la variation de x par la dérivée . On peut la noter

exemple
f(x)=x²+x
f'(x)=2x+1
f(2)=6
f'(2)=5


f(2,01) est donc estimée à 6+5*0.01=6.05
La valeur exacte de f(2.01) est 6.0501

[Anonyme]

Salut
La dérivée est la limite du taux de variation.
La différentielle de f en est l'application linéaire qui multiplie la variation de x par la dérivée . On peut la noter

exemple
f(x)=x²+x
f'(x)=2x+1
f(2)=6
f'(2)=5


f(2,01) est donc estimée à 6+5*0.01=6.05
La valeur exacte de f(2.01) est 6.0501

Donc, , on peut dire que df est le taux de '' sensibilité '' de f lors d'une petite variation dx de x ?

Et pour les intégrales ?

[Robic]

Tu demandais où était la fonction dans . Elle est présente... mais cachée. En fait, on intègre la fonction constante et égale à 1 : c'est où .

Concernant les , c'est juste une notation. Mais il existe des théorèmes qui justifient que certains bidouillages n'en sont pas.

Exemple : on sait que (ce n'est plus au programme de terminale S depuis l'an dernier, mais tu as peut-être déjà entendu parler ?). C'est un théorème. Maintenant, notons F la fonction f(g). Eh bien avec la notation , on pourrait écrire :

(j'ai juste multiplié en haut et en bas par la même quantité, dg).

Ici :
- , c'est F', c'est-à-dire la dérivée de f(g).
- , c'est la dérivée de F vu comme une fonction de g (et non pas comme une fonction de x, à cause du dg). Donc c'est f'.
- , c'est bien sûr g'.

Du coup on obtient :

et on retrouve bien la formule de la dérivée d'une fonction composée. Ça semble être un bidouillage avec les df et les dx, mais ça repose sur un théorème. En fait, c'est juste une notation pratique du théorème (mais ça n'en est pas sa démonstration).

[paquito]

Mathématiquement, la notation différentielle n'est pas correctement définie, puisque df et dx sont des
" infiniment petits ", notion qui ce qui n'est pas définie. Il faut donc prendre tout ça comme une notation bien pratique puisque ça marche bien!
Exemple pour la dérivée de f(u); df(u)/dx=df(u)/du*du/dx=f'(u)*u'.
Pour les intégrales, c'est une notation bien pratique aussi, par exemple quand on fait un changement de variable.
Pour le reste les raisonnements de physicien font toujours appel à une somme d'infiniment petits qui donnent une intégrale.
Exemple: calcul du volume d'une demie sphère de rayon R. on obtient des cylindres élémentaires de volumes:
dv=pi(R²-x²)dx et int(dv)=int(0; R)pi(R²-x²)dx=pi(R²x-x^3/3) entre 0 et R = pi(R^3-R^3)/3=(2/3)piR^3 et pour la sphère (4/3)piR^3.
Comme ça marche, c'est bon à prendre!

[Anonyme]

Merci pour ta réponse, j'ai mieux compris l'intégrale, par contre pour la dérivée, j'ai trouvé la bonne question :

J'ai vu deux '' définitions '' du

J'ai d'abord lu que le taux d'accroissement de la fonction f est :
Les signifiant une différence d'une même quantité.

La dérivée , avec les '' d '' exprimant un '' différentiel '' et sous entendant une différence infiniment petite d'une même quantité.

D'autres part, j'ai lu que la dérivée qui peut s'écrire : , que l'entité
était un '' opérateur '' différentiel qui agissait sur la fonction f.

Je viens de retrouver cette confusion en physique puisque je viens de lire (les auteurs l'ont écrit sans gêne, comme si c'était évident):

[Anonyme]

Tu demandais où était la fonction dans . Elle est présente... mais cachée. En fait, on intègre la fonction constante et égale à 1 : c'est où .

Concernant les , c'est juste une notation. Mais il existe des théorèmes qui justifient que certains bidouillages n'en sont pas.

Exemple : on sait que (ce n'est plus au programme de terminale S depuis l'an dernier, mais tu as peut-être déjà entendu parler ?). C'est un théorème. Maintenant, notons F la fonction f(g). Eh bien avec la notation , on pourrait écrire :

(j'ai juste multiplié en haut et en bas par la même quantité, dg).

Ici :
- , c'est F', c'est-à-dire la dérivée de f(g).
- , c'est la dérivée de F vu comme une fonction de g (et non pas comme une fonction de x, à cause du dg). Donc c'est f'.
- , c'est bien sûr g'.

Du coup on obtient :

et on retrouve bien la formule de la dérivée d'une fonction composée. Ça semble être un bidouillage avec les df et les dx, mais ça repose sur un théorème. En fait, c'est juste une notation pratique du théorème (mais ça n'en est pas sa démonstration).

C'est quel théorème qui permet ça ?

[paquito]

Il faut écrire g(x0+h)=g(x0)+g'(x0)h+he(h) où e(h)->0 quand h->0 et
f(X0+h)=f(X0)+f'(X0)h+he'(h)......

f((g(x0+h))=f(g(x0)+h(g'(x0)+e(h))=f(g(x0))+f'(g(x0))(g'(x0))h+h²(g'(x0)+e(h))+h(g'(x0)+e(h))e'(h)

Le résultat cherché est ce qui est facteur de h, soit f'(g(x0))(g'(x0); le terme suivant (à vérifier, je n'ai pas eu le courage de l'écrire) se mettant sous la forme he''(h).

Ce n'est pas drôle du tout et ça nécessite de modifier la définition de f'(x0) en posant
((f(x0+h)-f(x0))/h= f'(x0) +e(h) avec e(h)->0 quand h->0.

[chan79]

Tu peux essayer de retrouver le volume d'une demi-sphère en calculant



avec =rayon du cylindre hachuré (de hauteur dh)

Utilise
et

[Robic]

C'est quel théorème qui permet ça ?

Le théorème de dérivée des fonctions composées. Il n'est plus au programme de terminale depuis l'an dernier. On le trouve par exemple ici, page 5 : http://www.panamaths.net/Documents/SyntheseCours/SC_COMPLTDERIV_TS.pdf .

[Anonyme]

Et peut on vraiment appliquer les règles de calcul aux '' dx''?

Sur cette page, les auteurs ne se gênent pas, on retrouve ça pour la détermination de la dérivée particulaire :

Soit la différentielle :



D'où en multipliant par :



Ça me paraît un peu trop bricolé, et un peu trop abusif de parler de '' dérivée ''...

Même exemple, avec la détermination de l' équation horaire, où ils se basent sur l'égalité :



Un peu plus loin je retrouve le même concept pour des mouvements :




Ça fait beaucoup de bricolage tout de même ! Avec un peu de bidouillage des '' dt'', on peut faire apparaître une nouvelle grandeur.
Pour moi la dérivée c'est une fonction, pas le rapport de quantités infiniment petites. Pourtant ça à l'air le contraire.

[Robic]

Tout ça, c'est de la notation de physicien. Ça a l'air d'être du bricolage, mais ça repose sur de vrais théorèmes. C'est juste une façon d'écrire ces théorèmes qui est (considérée comme) pratique.

Il faut bien que tu comprennes qu'on ne démontre pas que égale la formule que tu as indiqué (flemme de la recopier...) en multipliant par \frac{1}{dt}. Si, les physiciens le font et croient c'est une démonstration. Mais les mathématiciens ont donné une définition précise de la différentielle qui fait que, après démonstration rigoureuse s'appuyant sur cette définition, on a la formule en question.

[Anonyme]

Tout ça, c'est de la notation de physicien. Ça a l'air d'être du bricolage, mais ça repose sur de vrais théorèmes. C'est juste une façon d'écrire ces théorèmes qui est (considérée comme) pratique.

Il faut bien que tu comprennes qu'on ne démontre pas que égale la formule que tu as indiqué (flemme de la recopier...) en multipliant par \frac{1}{dt}. Si, les physiciens le font et croient c'est une démonstration. Mais les mathématiciens ont donné une définition précise de la différentielle qui fait que, après démonstration rigoureuse s'appuyant sur cette définition, on a la formule en question.

Oui, sans doute, mais je trouve que ça porte plus à confusion qu'autre chose, à croire qu'il existe une dérivée pour '' physicien '' et une dérivée pour '' mathematicien''...
Le plus frappant, tout de même c'est sans doute que toutes ce bidouillage a l'air parfaitement naturel.

Tout ce que j'ai pris, je l'ai pris la: http://sciences.ch/htmlfr/mecanique/mecanclassique01.php

[busard_des_roseaux]

bonjour,
ces formules viennent du théorème des fonctions implicites. Au moins localement, tout est fonction de tout et on peut toujours écrire

la quantité z , fonction de x est fonction de y.

Il est possible que ça soit lié à la stricte monotonie des quantités,
exemple
prix du hamburger à Pékin ; poids de mon chat à New York
aujourd'hui : 2,60 ; 4,2
demain 2,70 ; 4,3
après demain 2,80 ; 4,4

ainsi le prix du hamburger à Pékin est fonction du poids de mon chat à New York

[Anonyme]

bonjour,
ces formules viennent du théorème des fonctions implicites. Au moins localement, tout est fonction de tout et on peut toujours écrire

la quantité z , fonction de x est fonction de y.

Il est possible que ça soit lié à la stricte monotonie des quantités,
exemple
prix du hamburger à Pékin ; poids de mon chat à New York
aujourd'hui : 2,60 ; 4,2
demain 2,70 ; 4,3
après demain 2,80 ; 4,4

ainsi le prix du hamburger à Pékin est fonction du poids de mon chat à New York

Tu veux dire qu'il existe toujours une fonction pour relier deux quantités ?

[Robic]

Oui, sans doute, mais je trouve que ça porte plus à confusion qu'autre chose, à croire qu'il existe une dérivée pour '' physicien '' et une dérivée pour '' mathematicien''...

C'est sensé être pratique pour les calculs. J'avoue que dans le cas des changements de variables, ça m'a servi. Par contre je ne trouve pas ça pratique pour comprendre. Et en maths, le but est de comprendre (les calculs, on les laisse aux physiciens...) Du coup je n'aime pas trop cette notation. Peut-être que tu es comme moi. Bon, on n'en meurt pas. Disons qu'on évite de faire des études de physique... (j'ai fait des études de maths appliquées, dont un très gros morceau était les équations aux dérivées partielles, eh bien on n'utilisait pas cette notation).

[busard_des_roseaux]

Tu veux dire qu'il existe toujours une fonction pour relier deux quantités ?

oui, dans les cas de monotonie (une fonction est juste une "flèche")

[busard_des_roseaux]

D'autres part, j'ai lu que la dérivée qui peut s'écrire :

ça non! si tu confonds une fonction f et une image f(x), même générique, tu risques des erreurs de logique parfois subtiles

[Anonyme]

ça non! si tu confonds une fonction f et une image f(x), même générique, tu risques des erreurs de logique parfois subtiles

J'ai lu que c'était équivalent et que on ommetait le (x) pour alléger l'écriture... Encore un truc de physicien !