Echantillonnage
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par busard_des_roseaux » 17 Mar 2014, 11:54
par busard_des_roseaux » 17 Mar 2014, 11:54
bonjour,
si l'on dispose d'un échantillon (de sa réalisation) , on dispose d'une série

de moyenne
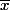
, de variance var(x)
Si l'on modèlise un échantillon aléatoire, on dispose de n variables aléatoires
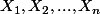
de moyenne
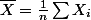
, de variance
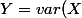=\frac{1}{n} \sum_i (X_i- \overline{X})^2)
d'écart-type
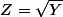
Si les

sont supposées indépendantes et de même loi , d'espérance
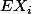
et de même variance
)
quelle sont l'espérance et la variance de
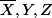
?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 17 Mar 2014, 13:14
par Sylviel » 17 Mar 2014, 13:14
Réponse partielle :
pour la moyenne empirique (\bar{X}):
la linéarité de l'espérance, et les propriétés de la variance pour une somme de variable indépendante te donne le résultat immédiatement.
Pour la variance empirique (Y) :
pour l'espérance il faut développer chaque terme pour raconnaitre partout des Var(Xi)
Pour la variance je ne sais pas...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités