Dans quelque temps auront lieux les Olympiades académiques de maths en 1°S et notre professeur nous a donné un petit exercice intéressant pour nous entraîner. (Nous y allons en touristes, juste pour voir!).
Cependant, je n'y arrive pas vraiment...
J'ai recopié l'énoncé complet:

J'ai répondu à la question 1, 2a et 2b. Je bloque totalement à la question 2c, j'ai juste remarqué qu'elle pouvait s'écrire
Pour la question 3, je ne suis pas sûr d'avoir compris tous les mots mais j'aurais dit que la valeur minimale était n/2. Je ne pense pas être capable de le démontrer mais ça me semblerait logique... A cet instant, cela signifierait que les termes seraient correctement ordonnés.
Pourriez-vous m'aider à répondre?

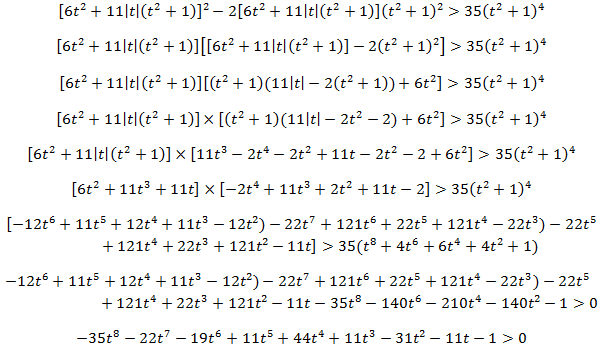 [/CENTER]
[/CENTER]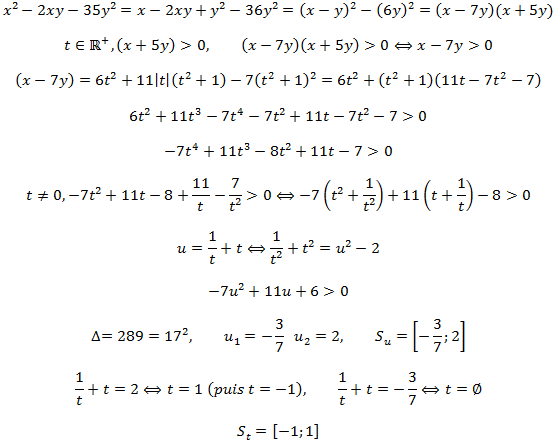 [/CENTER]
[/CENTER] [/CENTER]
[/CENTER] . Alors la somme vaut
. Alors la somme vaut  .
.