Espace vectoriel, endormorphisme

[wall]

Bonjour à tous,

J'ai besoin d'aide pour répondre aux questions suivantes :

Soit E un K-espace vectoriel. Soit p un projecteur de E, c'est-à-dire un endomorphisme de E vérifiant p o p = p.
1. Démontrer que ker p Im p = {0}
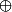
2. Pourquoi peut-on en déduire que E= ker p Im p ?
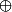
3. Démontrer que lorsque E est de dimension infinie on a encore E =ker p Im p

Avez vous des pistes pour commencer ? Je suis bloqué

Bonne soirée

[adrien69]

Salut, si y appartient à Im(p) comment peux-tu l'écrire ?

[wall]

J'ai réussi à faire les 2 premières questions, merci quand même

Pour la 3., c'est assez flou par contre ! Pour traiter le cas E de dimension infinie, dois-je le traiter comme un espace vectoriel qui n'est pas de dimension fini ? Et comment faire ?

[L.A.]

Bonsoir.

Dans le cas "dimension INfinie" tu ne peux plus utiliser le théorème du rang, il faut donc revenir à la définition brute des sommes directes et des supplémentaires.

[mrif]

J'ai réussi à faire les 2 premières questions, merci quand même

Pour la 3., c'est assez flou par contre ! Pour traiter le cas E de dimension infinie, dois-je le traiter comme un espace vectoriel qui n'est pas de dimension fini ? Et comment faire ?

Pour la 3), sans faire intervenir la dimension de E, tu commences par montrer que si x appartient à l'intersection de Im(p) et ker(p) alors x=0, ensuite que tout élément x de E peut s'écrire comme la somme d'un élément de Im(p) et d'un élément de ker(p).

Si x appartient à Im(p) alors il existe t tel que p(t) = x. On en déduit que p(p(t)) = p(x) = p(t) =x puisque pop=p et comme x apparteint à Ker(p), p(x) = 0. Donc x = 0, ce qui prouve la première partie.

Pour la 2 ème partie tu écris x = x-p(x) + p(x), tout en remarquant que x-p(x) appartient à ker(p).

[adrien69]

En fait la première partie est inutile étant donné que "somme directe" veut exactement dire qu'il doit y avoir une décomposition en somme de deux éléments et qu'elle doit être unique.

Sauf que si j'écris x=p(y)+a, avec a dans Ker(p), en appliquant p à l'égalité, p(x)=pop(y)=p(y), ce qui donne p(y) de manière univoque, valant p(x), et ensuite a ne peut qu'être x-p(x) en soustrayant simplement p(x). Y a plus qu'à montrer que x-p(x) est dans le noyau.

Il y a deux raisons pour lesquelles je préfère cette méthode :
1) elle est plus rapide
2) elle ne nous fait pas passer pour des magiciens qui sortons sans prévenir une décomposition de notre chapeau qui (oh ! Miracle !) marche.