Equation et suite

[Ben314]

Sinon, avec le à la place du 1, ça tente personne ?

Enoncé complet :
Soit fixé.
1) Montrer que, pour tout , l'équation admet une unique solution positive que l'on note .
2) Déterminer (en fonction de ) la limite de la suite

[Frede]

Allez, je suis preneur, à condition que:

- tu acceptes les solutions astucieuses, du style "le produit des racines est égal à a et à partir de n=4, leur somme est égale à 0, donc ... après je ne sais pas quoi, je chercherai". A mon grand âge, je n'aime plus que ça, je n'ai pas ta facilité pour manier l'artillerie lourde.

- je puisse utiliser ce qui a été trouvé dans le cas où a était égal à 1. En particulier pour la limite. Je pense qu'elle devient: "la plus petite des racines de x²+2x+a=0". (Si c'est pas ça, ce sera pas loin.)

- tu tolères quelques étourderies par ci par là.

- et si je peux marchander un peu, que a soit un rationnel.

[Ben314]

...tout ce que tu veut (a rationnel, toute méthode admise, etc...)

En fait, LA astuce, c'est que, par rapport au cas a=1, tout ne se passe pas toujours exactement de la même manière et le but c'est de voir où ça change quelque chose et... ce que ça change...

Par exemple (et justement en l'ocurence... :hein:) la limite de la sute un n'est pas toujours égale à la plus grande racine de x²+2x-a vu que cette dernière peut être >1 alors que la suite un est majorée par 1.

[Robic]

Comment ça la suite est majorée par 1 ?

Si je note f_n(x) = x^n + x² + 2x - a, on applique comme précédemment le théorème des valeurs intermédiaires pour obtenir l'unicité de la racine positive. Mais : f_n(1) = 4 - a, donc pour a > 4, f(1) est encore strictement négatif : la racine est donc >1.

J'imagine que la suite des racines est majorée, mais pas forcément par 1.

----
Après relecture, je crois que j'avais compris de travers (mais c'est pas très clair...). Tu veux dire qu'il est possible que la plus grande racine de x² + 2x - a soit > 1 et que, pour la même valeur de a, la suite (u_n) reste majorée par 1 (et non pas pour tout a) ?

La racine de x² + 2x - a est sqrt(1+a) - 1, donc elle est > 1 pour a > 3. Comme f_n(1) = 4 - a, on aura f_n(1) > 0 pour a dans ]3; 4[ et alors en effet la valeur de u_n sera strictement inférieure à 1.

OK, j'ai compris ! (Ça a l'air compliqué... :hein3: )

[Ben314]

J'ai effectivement écrit une connerie que... tu as rectifié...
Dans les cas où 3Le but c'est de comprendre où le raisonnement fait dans le cas a=1 déconne et de voir comment s'en sortir (et donc trouver la limite...)

[Robic]

Finalement je retape tout le message (disons que ce que j'ai tapé tout à l'heure, c'était le brouillon).

Je note . On suppose a > 0 (en fait a = 0 est possible, voir plus bas).

1) Les fonctions sont continues et strictement croissantes sur R+ en tant que sommes de fonctions strictement croissantes. De plus, on a :
.
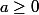
Le théorème des valeurs intermédiaires permet d'affirmer qu'il existe une unique racine de dans l'intervalle ]0;a[. (Si on suppose seulement , on obtient l'existence d'une unique racine dans [0;a].)

2) Soit x un réel positif. On a :
,
ce qui prouve que :
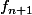
- si x 1 alors et la courbe de est au-dessus de la courbe de .
Il en résulte que :
(2.1) - si ,
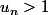
(2.2) - si alors pour tout n, donc est la suite constante égale à 0. En particulier elle tend vers 0.
- Si a = 4, alors pour tout n, donc est la suite constante égale à 1. En particulier elle tend vers 1.

5) Supposons que a appartient à ]0;3[.

On a : . On en déduit : , c'est m(a). On a donc : . Par le théorème des valeurs intermédiaires, on en déduit que . (Remarque : ce majorant que je prétend optimal est justement la limite conjecturée).

De plus, si 0 0 aussi petit qu'on veut, il est toujours possible de trouver n à partir duquel .

Un tel n existe, et il est de plus en plus grand à mesure que e diminue vers 0, donc quel que soit e>0 aussi petit qu'on veut, il existe un n à partir duquel est compris entre 1-e et 1, ce qui est équivalent à . Ainsi, la suite est minorée par 1. De plus, d'après (2.2), elle est décroissante. Elle admet donc une limite. Notons L cette limite, on sait que .

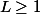
On va calculer L de la même façon que plus haut (là encore le dessin montre une branche de parabole de plus en plus verticale, d'ailleurs il est facile de vérifier que f'(1) tend vers l'infini). Soit e>0, on a (développement limité à l'ordre 1 similaire au précédent) :
,
donc si et seulement si .

Un tel n existe, et il est d'autant plus grand que e diminue vers 0, donc pour tout e>0 aussi petit qu'on veut, il existe un n à partir duquel la racine est comprise entre 1 et 1+e, ce qui est là encore équivalent à , et donc tend vers 1.

Bilan :
- Pour a de 0 à 3, u_n croît et tend vers .
- Pour a de 3 à 4, u_n croît et tend vers 1.
- Pour a supérieur à 4, u_n décroît vers 1.
(Les cas limites 0, 3 et 4 sont compatibles, il y a une continuité de la limite en fonction de a.)

C'était effectivement intéressant. (Ce que j'aime bien ici, c'est qu'il faut regarder la courbe pour avoir des idées. Sans dessin, je serais resté bloqué dès le début.)

[Frede]

C'est exactement ce que j'allais dire. Enfin, ce que j'aurais peut-être dit dans 3 ou 4 jours.

Le contrat est rempli et on n'a pas eu besoin de la concession que j'avais réussi à arracher ( a rationnel). J'aurais dû demander plus.

[Ben314]

Sur le principe, c'est tout à fait ça (en particulier, la remarque (*) est le point clef de la démonstration), mais il y a un bug dans ton raisonnement à la fin.
Tel le prof de base, je commence par des commentaires pas trés importants concernant le début :

- Dans le 1), la réponse "...une unique racine dans [0,a]" ne correspond pas à 100% à ce qui est demandé "... une unique racine positive", mais vu la stricte croissance de la fonction sur R+, c'est du kif-kif.

- Concernant les points (2.1) et (2.2), on peut remarquer que, de plus, comme fn(1)=4-a ne dépend que de a (et pas de n), soit a>=4 et tout les Un seront tous >=1 donc la suite sera croissante, soit a=1 et la suite sera décroissante : ce qui permet d'affirmer immédiatement que, dans tout les cas, elle converge.

- Au milieu du 5) tu écrit "...le terme x^n, du fait que x est ici 0 fixé qu'il faut estimer fn(1-e) lorsque n tend vers l'infini. Et là, il n'y a même pas besoin de D.L. : pour e>0 fixé, (1-e)^n tend vers 0 lorsque n->oo donc fn(1-e) tend vers (1-e)^2+2(1-e)-aN, on ait fn(1-e)1-e ce qui permet de conclure.

Bon, sinon, il y a une jolie façon de conclure un peu plus rapidement :
- Dans le cas a0 ce qui montre que Un1, le cas L=R est exclu dont on a forcément L=1.
- Idem pour le cas a>4, on sait que la suite est décroissante et minorée par 1 donc converge vers un L>=1.
De plus, pour tout n on a (Un)^n+Un²+2Un-a=0.
Comme (Un) est décroissante, sa limite L la minore et donc si L>1 alors L^n tend vers +oo donc (Un)^n aussi et la formule çi dessus est contradictoire. Donc on a forcément L=1.

Remarque : dans les cas où a>3 (donc L=1), la limite de (Un)^n est une forme indéterminée du style 1^oo mais on peut trés simplement lever l'indétermination en écrivant que (Un)^n=a-2Un-Un² qui tend vers a-3.
Cela permet d'avoir en plus une estimation de la vitesse de convergence : Un-L est équivalent à (ln(a-3))/n

[Robic]

Je savais qu'il y avait une erreur dans le 6) parce que s'il était vrai, la méthode pouvait s'appliquer aussi dans le 5) et alors on prouverait que tend vers 1 également si 03. Cette fois tout se tient !

(L'erreur avec le développement limité, c'était quand même subtil et j'ai du réfléchir un peu pour m'en persuader... :id: )

Au fait, puisqu'il n'y a pas eu besoin de développements limités, tout est faisable avec le programme de terminale. Est-ce qu'on peut donner ça comme sujet de bac ?... :bad2:

[Ben314]

Au fait, puisqu'il n'y a pas eu besoin de développements limités, tout est faisable avec le programme de terminale. Est-ce qu'on peut donner ça comme sujet de bac ?... :bad2:

Je susi pas persuadé qu'avec ça on aurait 92.5% de taux de réussite au bac S.
En particulier, un truc marrant (si on peut dire) que j'ai constaté concernant l'exo (que j'ai posé assez souvent à un moment de ma carrière), c'est la difficulté à montrer par exemple que la suite Un est croissante sachant que la suite fn est décroissante et que les fn sont toutes croissantes. Des tas d'étudiants n'y arrivent pas du tout :déjà un bon paquet ont beaucoup de mal à comprendre que fn puise être à la fois "croissante" et "décroissante"...
Et les "bons" (qui ont pensé à faire un dessin...) arrivent souvent à la seule conclusion que "ça se voit bien sur le dessin". C'est (nettement) mieux que rien, mais, bon...

[Robic]

Chouette, je fais partie des bons puisque je n'ai pas pris la peine de démontrer ça vu que ça se voit sur le dessin... :zen:

(Mais je vois comment le démontrer. Il suffit de partir de la racine u_n de f_n et remarquer que si f_{n+1} < f_n alors f_{n+1}(u_n) < 0, donc, par le théorème des valeurs intermédiaires, la racine u_{n+1} de f_{n+1} est plus grande que u_n.)

[Ben314]

Tient, sinon, un truc que j'arive pas trop à voir, c'est la vitesse de convergence de la suite dans le cas a=3 (i.e. un équivalent assez simple de Un-L avec ici L=1)
Pour les autres valeurs de a, c'est plutôt simple, mais là... :cry: