Bonjour, je dois rendre un DM pour la rentré. Malheureusement, je suis bloquée sur certaines questions. Voici le sujet :
Le plan complexe est muni d'un repère orthonormal direct (O;u,v). On prendra pour unité graphique 4 cm.
On pose z0 = 2 et, pour tout entier naturel n, zn+1=(1+i)/2*zn. On note An le point du plan d'affixe zn.
1.Déterminer les formes algébriques et exponentielles de z0, z1, z2, z3, z4.
Placer les points A0, A1, A2, A3 et A4 sur une figure. et on admet que : z5=-1/4-1/4i.
2.Pour tout entier naturel n, on pose : an=arg(zn)
a. Interpréter goémétriquement an. En utilisant le graphique, conjecturer une relation entre an+1 et an.
b.Démontrer que (an) est une suite arithmétique; en déduire que, pour tout entier naturel n, on a : an=n*pi/4
3. Pour tout entier naturel n, on pose dn = |zn|.
a. Démontrer que dn est une suite géo de raison racine carré de 2/2, puis exprimer dn en fonction de n. Déterminer la limite de la suite dn.
b.Interpréter géographiquement dn, puis les résultats de la question a.
4. Déduire des questions précédentes la forme trigo et algé de z18.
5.a.Quelle semble etre la nature des triangles OAnAn+1?
b.Déterminer la forme algé, puis trigo du quotient : (zn+1-zn)/zn+1 (n étant un entier naturel quelconque).
c. En déduire, pour tout entier naturel n, la nature du triangle OAnAn+1.
6.Un prolongement:
Pour tout entier naturel n supérieur ou égal à 1, on pose ln=An-1An
Démontrer que, pour tout entier naturel non nul, on a ln+1=2/2ln. Exprimer ln en fonction de n.
Pouvais vous m'aider à la 5.b, svp ?
Devoir maison nombres complexes et suites
3 messages
- Page 1 sur 1
Salut !
Pour tout ,
,  donc exprime le quotient
donc exprime le quotient  sous la forme
sous la forme 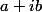 , où
, où  et
et  désignent deux réels quelconques.
désignent deux réels quelconques.
(A titre informatif, que trouves-tu pour la 5.a. ?)
mmargaux a écrit:5.a.Quelle semble etre la nature des triangles OAnAn+1?
b.Déterminer la forme algé, puis trigo du quotient : (zn+1-zn)/zn+1 (n étant un entier naturel quelconque).
Pour tout
(A titre informatif, que trouves-tu pour la 5.a. ?)
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Salut !
Pour tout ,
,  donc exprime le quotient
donc exprime le quotient  sous la forme
sous la forme 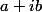 , où
, où  et
et  désignent deux réels quelconques.
désignent deux réels quelconques.
(A titre informatif, que trouves-tu pour la 5.a. ?)
mmargaux a écrit:5.a.Quelle semble etre la nature des triangles OAnAn+1?
b.Déterminer la forme algé, puis trigo du quotient : (zn+1-zn)/zn+1 (n étant un entier naturel quelconque).
Pour tout
(A titre informatif, que trouves-tu pour la 5.a. ?)
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
