Equation et suite
32 messages
- Page 1 sur 2 - 1, 2
Equation et suite
Bonjour tout le monde ! Je suis en prépa bio et je bloque à un exo de math..
L'énoncé :
1)Montrer que pour tout n>=3, x^n+x²+2x-1=0 a une unique solution notée u(n).
j'ai procédé par récurrence, j'ai réussi l'initialisation pour n=3 mais pour l'hérédité je bloque..
2) Montrer que u(n) est croissant est minorée par 1/2
Vu que j'ai pas réussi la 1)...
Quelqu'un pourrait me filer un coup de main? :we:
L'énoncé :
1)Montrer que pour tout n>=3, x^n+x²+2x-1=0 a une unique solution notée u(n).
j'ai procédé par récurrence, j'ai réussi l'initialisation pour n=3 mais pour l'hérédité je bloque..
2) Montrer que u(n) est croissant est minorée par 1/2
Vu que j'ai pas réussi la 1)...
Quelqu'un pourrait me filer un coup de main? :we:
L'équation peut s'écrire
^2 = 0)
ou
^2)
Donc une racine ayant une grande valeur, par exemple x=25 est exclue car si n>3, x à la puissance 4 par exemple ne peut pas être égal à -(x-1)^2
Mais l'équation peut aussi s'écrire:
^2)
ou
^2}{x^2} \)
Or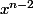 ne peut être négatif que si x est négatif et n impair.
ne peut être négatif que si x est négatif et n impair.
On peut aussi écrire:

De plus, dans toute équation de degré n, le dernier terme, (ici: -1) est le produit des racines.
J'avoue ne rien voir de plus ce soir, mais peut-être que ça peut t'aider à démarrer.
ou
Donc une racine ayant une grande valeur, par exemple x=25 est exclue car si n>3, x à la puissance 4 par exemple ne peut pas être égal à -(x-1)^2
Mais l'équation peut aussi s'écrire:
ou
Or
On peut aussi écrire:
De plus, dans toute équation de degré n, le dernier terme, (ici: -1) est le produit des racines.
J'avoue ne rien voir de plus ce soir, mais peut-être que ça peut t'aider à démarrer.
bbop a écrit:1)Montrer que pour tout n>=3, x^n+x²+2x-1=0 a une unique solution notée u(n).
Soit la fonction
L'existence d'une solution de l'équation
L'unicité résulte de la strictement monotonie de la fonction
2) Montrer que u(n) est croissant est minorée par 1/2
La croissance de la suite
Ouais, calculer la dérivée, ça peut apporter quelque chose mais il faut prendre la dérivée seconde pour arriver à trouver des racines et ensuite voir si la dérivée est croissante. Je ne vois pas comment aller plus loin. Elle est pas marrante ta solution.
Oui mais là tu supposes que l'énoncé est juste, or il est faux. Si, comme le soupçonne Ben314, il faut se limiter aux x positifs, alors sa méthode est on ne peut plus simple : la dérivée suffit, et la réponse se voit aussitôt. (Et SaintAmand a raison : même pas la peine de dériver, on voit qu'on a une somme de fonctions croissantes.)
Maintenant, est-ce que son soupçon est justifié. Oui : par la deuxième question ! La suite ainsi définie est sensée être majorée par 1/2, donc il s'agit de la solution positive. (Oui, je sais, bbop a dit « minorée ». Mais bbop est distrait : si la suite était croissante minorée, on ne pourrait rien en conclure. Or il est facile de démontrer que la suite est majorée par 1/2 donc c'est sûrement ce qu'il voulait dir.)
(C'est un nouveau jeu : reconstituer l'énoncé correct... :ptdr: )
Oui j'étais un peu distraite haha vous avez raison !
Pour le 1à) c'est bien une solution dans R+ et puor le 2) c'est bien croissante et majorée par 1/2 ! :ptdr:
Mais enfaite je ne vouis pas comment déduire la monotonie de u(n) et sa majoration en fonction de f(x)=x^n+x²+2x-1.. Enfin proprement ! Et je ne vois pas comment le déduire du tableau de la question 1)..
Saint Amand :
Pour le 1à) c'est bien une solution dans R+ et puor le 2) c'est bien croissante et majorée par 1/2 ! :ptdr:
Mais enfaite je ne vouis pas comment déduire la monotonie de u(n) et sa majoration en fonction de f(x)=x^n+x²+2x-1.. Enfin proprement ! Et je ne vois pas comment le déduire du tableau de la question 1)..
Saint Amand :
Mais moi je trouve que la focntion fn(x) est croissante......La croissance de la suite (u_n) résulte de la décroissance de la suite (f_n(x)) pour tout x\in[0,1/2]
La majoration n'est pas difficile. Place dans le tableau de variation la valeur x = 1/2 et son image par f. Tu constates que f(0) est négatif mais f(1/2) est positif, donc la racine est forcément comprise dans l'intervalle [0 ; 1/2], autrement dit u_n est compris entre 0 et 1/2.
Le fait que la suite (u_n) est croissante est plus difficile et se prouve comme l'a dit SaintAmand. Attention : la fonction f_n est en effet croissante mais la suite (f_n(x)) est décroissante. Ne confonds pas les deux :
- La fonction f_n est une fonction qui, à tout x, associe f_n(x). (Et d'ailleurs f_n(x) n'est pas une fonction, c'est un nombre !).
- La suite (f_n(x)) est la suite f_1(x), f_2(x), f_3(x), f_4(x)... où x est fixé. C'est une suite de nombres (d'images du même antécédent par les f_n successifs).
Pour comprendre comment ça marche, tu peux par exemple prouver que pour tout x entre 0 et 1/2 on a \leq f_n(x)) . Ça signifie que la courbe de la fonction
. Ça signifie que la courbe de la fonction 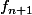 est en-dessous de la courbe de la fonction
est en-dessous de la courbe de la fonction  sur l'intervalle [0 ; 1/2]. Fais un dessin : tu verras alors que la racine de
sur l'intervalle [0 ; 1/2]. Fais un dessin : tu verras alors que la racine de 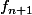 est forcément plus grande que celle de
est forcément plus grande que celle de  .
.
Le fait que la suite (u_n) est croissante est plus difficile et se prouve comme l'a dit SaintAmand. Attention : la fonction f_n est en effet croissante mais la suite (f_n(x)) est décroissante. Ne confonds pas les deux :
- La fonction f_n est une fonction qui, à tout x, associe f_n(x). (Et d'ailleurs f_n(x) n'est pas une fonction, c'est un nombre !).
- La suite (f_n(x)) est la suite f_1(x), f_2(x), f_3(x), f_4(x)... où x est fixé. C'est une suite de nombres (d'images du même antécédent par les f_n successifs).
Pour comprendre comment ça marche, tu peux par exemple prouver que pour tout x entre 0 et 1/2 on a
Ca y est j'ai compris ! Pour démontrer la monotonie j'ai fait comme ça :
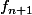 <
< car pour tout x
car pour tout x  [0;1/2],
[0;1/2],  . Donc la fontion
. Donc la fontion  décroit plus vite que la fonction
décroit plus vite que la fonction 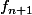 et donc la racine de TEX]f_n[/TEX] sera plus grande que la racine de
et donc la racine de TEX]f_n[/TEX] sera plus grande que la racine de 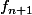 d'ou la suite u(n) est croissante !
d'ou la suite u(n) est croissante !
A la dernière question il demande la limite de la suite (oui je suis étourdie je l'ai oubliée..). J'aurais dit que cette suite u(n) tend vers 0 quand n tend vers + mais je ne saurais pas comment le prouver !
mais je ne saurais pas comment le prouver !
A la dernière question il demande la limite de la suite (oui je suis étourdie je l'ai oubliée..). J'aurais dit que cette suite u(n) tend vers 0 quand n tend vers +
Deltab : tu devrais lire les messages précédents... :lol3:
bbop : ton raisonnement est faux puisque les fonctions f_n ne sont pas décroissantes. (Tu as probablement compris l'idée mais tu l'exprimes mal). Pour démontrer que < f_n(x)) , il n'y a pas aussi des n et des n+1 à gérer ?
, il n'y a pas aussi des n et des n+1 à gérer ?
Sinon, u_n est croissante et majorée par 1/2, donc elle ne va pas tendre vers 0 ! (Ça, c'est si elle était décroissante et minorée). Peut-être qu'elle tend vers 1/2 ? Dans beaucoup d'exercices, quand on trouve un majorant, c'est la limite. En fait, si la suite tend vers l, alors f_n(l) tend forcément vers 0 (puisque u_n est la racine). Donc une idée pourrait être de chercher un x tel que f_n(x) tende vers 0 (mais je n'ai pas essayé).
bbop : ton raisonnement est faux puisque les fonctions f_n ne sont pas décroissantes. (Tu as probablement compris l'idée mais tu l'exprimes mal). Pour démontrer que
Sinon, u_n est croissante et majorée par 1/2, donc elle ne va pas tendre vers 0 ! (Ça, c'est si elle était décroissante et minorée). Peut-être qu'elle tend vers 1/2 ? Dans beaucoup d'exercices, quand on trouve un majorant, c'est la limite. En fait, si la suite tend vers l, alors f_n(l) tend forcément vers 0 (puisque u_n est la racine). Donc une idée pourrait être de chercher un x tel que f_n(x) tende vers 0 (mais je n'ai pas essayé).
Oui mais ça ne doit pas faire 0 ! (Ne lis pas trop vite mes réponses, je les modifie quand il y a des erreurs... ) J'ai essayé quelque chose mais ça ne marche pas.
Ah si ça marche, j'avais fait une erreur de signe !
Voilà l'idée intuitive : on cherche un nombre l compris entre 0 et 1/2 qui est la racine (positive), en quelque sorte, de = x^\infty + x^2 + 2x - 1) . Comme
. Comme  est nul (vu que x est compris entre 0 et 1/2), notre nombre l est la racine (positive) de
est nul (vu que x est compris entre 0 et 1/2), notre nombre l est la racine (positive) de  = x^2 + 2x - 1) . La racine d'un trinôme est facile à calculer, ici on trouve
. La racine d'un trinôme est facile à calculer, ici on trouve 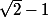 . C'est sûrement la limite cherchée.
. C'est sûrement la limite cherchée.
Reste à rédiger une vraie démonstration, par exemple en remplaçant mes infinis par des limites. (Mais le plus intéressant, je trouve, c'est de comprendre le raisonnement qui mène à découvrir cette limite...)
Ah si ça marche, j'avais fait une erreur de signe !
Voilà l'idée intuitive : on cherche un nombre l compris entre 0 et 1/2 qui est la racine (positive), en quelque sorte, de
Reste à rédiger une vraie démonstration, par exemple en remplaçant mes infinis par des limites. (Mais le plus intéressant, je trouve, c'est de comprendre le raisonnement qui mène à découvrir cette limite...)
Bonjour
C'est pour ça que j'ai effacé mon 1er message.
Si on récapitule le tout:
1- les fonctions sont strictement croissantes sur
sont strictement croissantes sur  (comme somme de 2 fonctions strictement croissantes en l'occurrence
(comme somme de 2 fonctions strictement croissantes en l'occurrence  et
et  (SaintAmand).
(SaintAmand).
2- L'existence de la solution de=0) dans [0,1/2] est assurée par la continuité de
dans [0,1/2] est assurée par la continuité de  et
et f_n(1/2)<0) et dans ce cas
et dans ce cas  . L'unité elle est assurée par la stricte croissance de la fonction
. L'unité elle est assurée par la stricte croissance de la fonction  (SaintAmand)
(SaintAmand)
3- Pour tout<f_{n}(x)) (bbop)
(bbop)
Si (u_n) est décroissante on aura pour tout
<f_{n+1}(x)<f_{n+1}(x_n)<f_{n}(x_{n})=0)
Si , on aurait eu
, on aurait eu 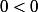
Si , alors
, alors =f_{n}(x_{n})) ce qui donne
ce qui donne 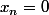 ou
ou 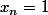 mais ni
mais ni  ni
ni  ne sont solutions de
ne sont solutions de =0) .
.
Reste à conclure ce qui ne pose plus de problèmes.
Robic a écrit:Deltab : tu devrais lire les messages précédents... :lol3:
C'est pour ça que j'ai effacé mon 1er message.
Si on récapitule le tout:
1- les fonctions
2- L'existence de la solution de
3- Pour tout
Si (u_n) est décroissante on aura pour tout
Si
Si
Reste à conclure ce qui ne pose plus de problèmes.
Une fois que tu as montré que
1) La suite de fonction fn est décroisssante (sur [0,1])
2) Chaque fonction fn est strictement croissante (sur [0,1])
Il te suffit d'écrire que
1)<f_n(u_n)=0=f_{n+1}(u_{n+1}))
et la stricte croissance de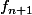 te permet d'en déduire que
te permet d'en déduire que 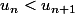
(l'idéal, c'est de faire un dessin avec les courbes des fonction fn et f{n+1} pour voir que... c'est trivial...)
1) La suite de fonction fn est décroisssante (sur [0,1])
2) Chaque fonction fn est strictement croissante (sur [0,1])
Il te suffit d'écrire que
1)
et la stricte croissance de
(l'idéal, c'est de faire un dessin avec les courbes des fonction fn et f{n+1} pour voir que... c'est trivial...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
