Tétraèdre coupé en deux

[chan79]

Niveau lycée, même si les notions utiles sont de niveau collège.(ne pas donner la réponse trop vite)
ABCS est un tétraèdre régulier d'arête 1.
M est un point de [SA] et N est un point de [SC] et (MN) est parallèle à (AC).
On pose x=SM.
Calculer x pour que le plan BMN partage le tétraèdre en deux parties de même volume.

[Imod]

Bonjour Chan

Sauf erreur le solide est coupé en deux pyramides de même hauteur et de bases SMN et AMNC qui doivent donc avoir la même aire . C'est à dire que l'aire de SMN doit être la moitié de celle de SAC donc .

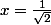
Imod

[chan79]

Bonjour Chan

Sauf erreur le solide est coupé en deux pyramides de même hauteur et de bases SMN et AMNC qui doivent donc avoir la même aire . C'est à dire que l'aire de SMN doit être la moitié de celle de SAC donc .

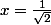
Imod

oui, Imod :zen:
Même question si la base est un carré (toutes les arêtes égales à 1)

[Imod]

Là je vais laisser faire les jeunes :zen:

Imod

[Ben314]