Mesure de Lebesgue
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 04 Mar 2014, 22:44
par barbu23 » 04 Mar 2014, 22:44
Bonsoir,
Dans l'exercice suivant, je bloque à la deuxième question :
Soient

et

deux réels et

définie par
=ax+b$)
.
)
Montrer que pour tout borélien
$)
, on a
 \in \mathcal{B}(\mathbb{R})$)
)
Montrer que pour tout borélien
$)
, on a
)=|a| \lambda (A)$)
J'ai réussi à faire la première question, mais je bute encore sur la deuxième question.
Merci d'avance pour votre aide. :happy3:
Edit : Pour la question
)
, c'est simple. En effet :
)
:
 = ( f^{-1} )^{-1} ( A ))
et

mesurable ( continue, bijective )
Edit :
 ) = \int_{f(A)} d \lambda = \int \mathbf 1_{f(A)} d \lambda = \int \mathbf 1_{f^{-1} ( f(A) ) } ( f (x) ) | \frac{ \partial f }{\partial x} (x) | d \lambda)
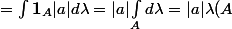)
J'ai appliqué la formule de changement de variables par rapport au difféomorphisme
 = ax + b)
Est ce que c'est correct ?
Merci d'avance. :happy3:
-
mr_pyer
- Membre Relatif
- Messages: 137
- Enregistré le: 07 Avr 2013, 20:42
-
 par mr_pyer » 05 Mar 2014, 08:21
par mr_pyer » 05 Mar 2014, 08:21
Oui c'est correct mais le théorème est beaucoup trop fort pour faire ce que l'on te demande (en fait on utilise ce que tu veux démontrer dans la démo du théorème).
Tu pourrais commencer par montrer que la formule marche avec les intervalles...
-
Alasdair
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Mar 2014, 03:53
-
 par Alasdair » 05 Mar 2014, 12:08
par Alasdair » 05 Mar 2014, 12:08
Pour la question 1), je ne le ferais pas comme ça puisque la question est essentiellement "montrer que

est mesurable" et que c'est l'argument que tu utilises. Comme ta fonction est monotone
 = [d, +\inf[)
, hors les intervalles

engendrent les boréliens donc avec un lemme du transport c'est bouclé.
Pour la 2), ça marche mais ça dépend de ce qu'on s'autorise (pour démontrer le théorème de changement de variable on a besoin en essence de la propriété que tu veux montrer). Pour t'en tirer avec les propriétés de base de la mesure de Lebesgue, prends un pavé P et montres que
) = |a|\lambda(P))
(avec l'invariance sous translation de la mesure de Lebesgue pour se débarrasser du b). Ensuite tu recouvres f(A) de pavés avec un recouvrement dont tu peux controler l'erreur via un epsilon ça te donnes une borne sup sur la mesure de f(A) qui converge vers |a|f(A). Et plus qu'à faire de même pour la borne inf' (ce qui se fait bien avec des passages au complémentaire).
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 12:40
par barbu23 » 05 Mar 2014, 12:40
Pouvez vous ce qui ne marche pas avec précision dans la démonstration que j'ai proposé ? Je n'ai pas bien saisi vos commentaires tous les deux.
Merci d'avance.
-
Alasdair
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Mar 2014, 03:53
-
 par Alasdair » 05 Mar 2014, 12:58
par Alasdair » 05 Mar 2014, 12:58
Ma remarque (et celle de mr_pyer) c'est que tu utilises des outils qui sont construits en partie par les choses que tu veux démontrer. Du coup c'est comme si on te demandais de fabriquer une lentille pour un microscope, et que tu prenais un microscope déjà existant et en retirerait la lentille. C'est "juste", on a bien la lentille voulue, mais ce n'est pas vraiment ce qu'on voulait que tu fasses.
Par opposition, dans ce que je proposais, j'essaye de n'utiliser que la définition de la mesure de Lebesgue (plus petite mesure qui complète et coïncide avec les volumes des pavés) et de celle des boréliens (tribu engendrée par les pavés) (et ces définitions t'indiquent la voie à suivre).
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 13:02
par barbu23 » 05 Mar 2014, 13:02
Ma remarque (et celle de mr_pyer) c'est que tu utilises des outils qui sont construits en partie par les choses que tu veux démontrer.
J'ai pas compris ça. :happy3:
Peux tu être plus précis stp ?
Merci d'avance. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 13:24
par barbu23 » 05 Mar 2014, 13:24
ça veut dire que je ne peux pas utiliser le théorème de changement de variables puisqu'il repose sur les résultats préétablis de l'exercice ? Mais, je vois mal le lien en réalité. :mur:
-
Alasdair
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Mar 2014, 03:53
-
 par Alasdair » 05 Mar 2014, 13:32
par Alasdair » 05 Mar 2014, 13:32
Dans le théorème de changement de variables tu as ce que tu veux démontrer qui y est directement inclus, sous une forme plus forte (remplace le a par le déterminant de la jacobienne). Du coup, tu vois que dans la démonstration du théorème de changement de variables à partir des définitions des différents éléments impliqués (mesure de lebesgue, définition de l'intégrale, boréliens, différentielle etc...) tu retrouverais une démonstration plus forte de ce que tu veux montrer.
Dans le cadre de l'exercice où l'on cherche à comprendre pourquoi les choses sont comme ça, je trouve qu'on passe à côté du sens profond en appelant un résultat plus fort. C'est comme si un vieux sifu te confisquait ton lance pierre et te demandait de descendre une cible (dans l'intention de te faire reconstruire un lance pierre pour comprendre comment il est fait), et qu'à la place tu prenais le bazooka de la réserve. Ca marche, mais ton sifu risque d'être déçu (ça devient n'importe quoi mes métaphores).
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 15:27
par barbu23 » 05 Mar 2014, 15:27
D'accord. :happy3:
De toute façon, est ce que si on nous donne le même exercice à l'examen, et je réponds de la même manière que mon premier poste, est ce que je risque de perdre des points ?
Merci d'avance. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 15:42
par barbu23 » 05 Mar 2014, 15:42
Alasdair a écrit:Pour t'en tirer avec les propriétés de base de la mesure de Lebesgue, prends un pavé P et montres que
) = |a|\lambda(P))
(avec l'invariance sous translation de la mesure de Lebesgue pour se débarrasser du b). Ensuite tu recouvres f(A) de pavés avec un recouvrement dont tu peux controler l'erreur via un epsilon ça te donnes une borne sup sur la mesure de f(A) qui converge vers |a|f(A). Et plus qu'à faire de même pour la borne inf' (ce qui se fait bien avec des passages au complémentaire).
Tu peux étayer un peu plus tes propos ?
Merci d'avance. :happy3:
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 05 Mar 2014, 15:57
par SLA » 05 Mar 2014, 15:57
barbu23 a écrit:Tu peux étayer un peu plus tes propos ?
Merci d'avance. :happy3:
On est sur

, donc vérifie que ta formule est vrai sur les intervalles, puis passe aux borélien. Proprement, pas en demandant aux autres de le faire.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 16:04
par barbu23 » 05 Mar 2014, 16:04
D'accord, c'est un peu étrange ce calcul je trouve :
On a :
) = \lambda ( a [x,y[ + b ) = \lambda ( [ax + b , ay + b [ ))
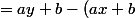 = a ( y - x ) = a \lambda ( [ x , y [ ))
mais, je n'obtiens pas :
) = |a| \lambda ( [ x , y [ ))
:hein:
-
Alasdair
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Mar 2014, 03:53
-
 par Alasdair » 05 Mar 2014, 16:11
par Alasdair » 05 Mar 2014, 16:11
La mesure de Lebesgue n'est pas une application linéaire, du coup ton calcul n'a pas de sens (et c'est exactement pour ça qu'il vaut mieux que tu fasses la question "pour de vrai", comme ça tu comprendra ce qu'il se passe et les objets que tu manipules). A la place, part de la définition de la mesure de Lebesgue (elle coïncide avec le volume sur les pavés).
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 16:15
par barbu23 » 05 Mar 2014, 16:15
Alasdair a écrit:La mesure de Lebesgue n'est pas une application linéaire, du coup ton calcul n'a pas de sens (et c'est exactement pour ça qu'il vaut mieux que tu fasses la question "pour de vrai", comme ça tu comprendra ce qu'il se passe et les objets que tu manipules). A la place, part de la définition de la mesure de Lebesgue (elle coïncide avec le volume sur les pavés).
Je n'ai pas compris ce que vous dites ... Ici, on est sur

, et sur

, la mesure de Lebesgue est définie par :
 = y - x)
.
-
Alasdair
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Mar 2014, 03:53
-
 par Alasdair » 05 Mar 2014, 16:18
par Alasdair » 05 Mar 2014, 16:18
Et pour la suite, une fois que tu as vérifié ta formule sur des éléments de base (les pavés), il faut bricoler avec ces pavés pour pouvoir toucher n'importe quel borélien. Deux choses viennent à l'esprit, utiliser le fait que les boréliens sont engendrés par les pavés, ou utiliser les pavés pour encadrer le borélien que tu veux mesurer. A toi d'essayer, et dis nous si tu bloques :),
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 16:21
par barbu23 » 05 Mar 2014, 16:21
Alasdair a écrit:La mesure de Lebesgue n'est pas une application linéaire, du coup ton calcul n'a pas de sens (et c'est exactement pour ça qu'il vaut mieux que tu fasses la question "pour de vrai", comme ça tu comprendra ce qu'il se passe et les objets que tu manipules). A la place, part de la définition de la mesure de Lebesgue (elle coïncide avec le volume sur les pavés).
Pourquoi tu dis que mon calul n'a pas de sens ? Peux tu donner plus de précisions sur ça ?
Merci d'avance. :happy3:
-
Alasdair
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Mar 2014, 03:53
-
 par Alasdair » 05 Mar 2014, 16:23
par Alasdair » 05 Mar 2014, 16:23
barbu23 a écrit:Je n'ai pas compris ce que vous dites ... Ici, on est sur

, et sur

, la mesure de Lebesgue est définie par :
 = y - x)
.
On est en dimension 1, donc on peut remplacer "pavés" par intervalles. Mais l'important, c'est que la mesure de Lebesgue coïncide avec un volume, et donc la formule que tu as écris plus haut est vraie seulement si x<y. D'où le petit manque de valeur absolue avec lequel tu te retrouvais.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Mar 2014, 16:26
par barbu23 » 05 Mar 2014, 16:26
Oui, mais dès qu'on écrit

, il est sous entendu que
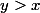
, ça a un sens d'écrire

avec
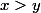
?
Tu veux dire qu'il faut écrire :
 = | x - y |)
? ça existe ça ?
-
Alasdair
- Membre Naturel
- Messages: 24
- Enregistré le: 04 Mar 2014, 03:53
-
 par Alasdair » 05 Mar 2014, 16:33
par Alasdair » 05 Mar 2014, 16:33
barbu23 a écrit:Oui, mais dès qu'on écrit

, il est sous entendu que
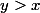
, ça a un sens d'écrire

avec
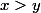
?
Tu veux dire qu'il faut écrire :
 = | x - y |)
? ça existe ça ?
Soit il faut faire ça, soit il faut faire gaffe quand tu multiplie ton intervalle par a et distinguer les cas a positif et a négatif. Et comme on parle de volume, il serait difficile de se retrouver avec un volume négatif, ce qui justifie la valeur absolue.
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 05 Mar 2014, 16:34
par SLA » 05 Mar 2014, 16:34
barbu23 a écrit:Oui, mais dès qu'on écrit

, il est sous entendu que
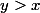
, ça a un sens d'écrire

avec
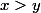
?
Tu veux dire qu'il faut écrire :
 = | x - y |)
? ça existe ça ?
Dans ce cas quand
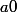
et
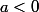
.
Dis toi bien que quand ta preuve ne donne pas le bon résultat, c'est pas que c'est faux, c'est que tu t'es trompé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
