Intégration par parties.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sheeppowa
- Membre Naturel
- Messages: 45
- Enregistré le: 26 Juil 2013, 10:23
-
 par Sheeppowa » 04 Mar 2014, 11:28
par Sheeppowa » 04 Mar 2014, 11:28
Bonjour à tous et à toute, j'ai un peu de mal pour cette intégrale :

J'ai donc posé :

et
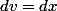
D'ou :
^2})dx)
Donc :
^2})dx)
D'ou :
^2}dx)
Or
^2}=(\frac{x^2}{x^2-1})^2)
Donc rebelote ...

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Mar 2014, 11:34
par chan79 » 04 Mar 2014, 11:34
salut
essaie une autre écriture du genre

-
Sheeppowa
- Membre Naturel
- Messages: 45
- Enregistré le: 26 Juil 2013, 10:23
-
 par Sheeppowa » 04 Mar 2014, 11:51
par Sheeppowa » 04 Mar 2014, 11:51
chan79 a écrit:salut
essaie une autre écriture du genre

Quel dommage que l'on ne nous apprenne pas la développement en éléments simples..
Si je suis ton raisonnement : k=-1/2, k'=1/2.
Et j'obtiens :
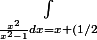ln(\frac{x-1}{x+1}))
Merci à toi


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Mar 2014, 15:24
par chan79 » 04 Mar 2014, 15:24
Sheeppowa a écrit:Quel dommage que l'on ne nous apprenne pas la développement en éléments simples..
Si je suis ton raisonnement : k=-1/2, k'=1/2.
Et j'obtiens :
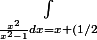ln(\frac{x-1}{x+1}))
Merci à toi

Rajouter des valeurs absolues
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 05 Mar 2014, 19:32
par deltab » 05 Mar 2014, 19:32
Bonjour.
L'intégrale peut effectivement se calculer par IPP (3IPP) en posant

et

. L'intégrale obtenue se calcule aussi par IPP en écrivant
= \ln(|x-1|)+ \ln(|x+1|))
. Il reste quand même que la décomposition en éléments est plus simple et plus rapide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités