Bonjour,
J'ai un polygone de n côtés dont je connais les coordonnées des points-côtés. Comment connaître l'ordre de succession de ces points sur le polygone, qui peut être connexe ou non ? Merci pour votre aide.
Retrouver la succession des sommets d'un polygone
13 messages
- Page 1 sur 1
Salut,
Y'a un truc qui m'échape : si ton polygone peut être connexe ou non, je vois vraiment pas comment tu va pouvoir retrouver quoi que ce soit dans l'ordre des sommets.
Pour moi, c'est un peu comme si tu demandait dans quel ordre tu as rangé les entiers de 1 à 10 en donnant comme seule information "il est possible qu'ils ne soient pas dans l'ordre" : ç'est un peu "short" comme info...
P.S. En plus, un polygône "non connexe", je suis pas sûr que ça ait bien du sens ce truc là : si c'est pas connexe, c'est que tu as plusieurs polygône...
Y'a un truc qui m'échape : si ton polygone peut être connexe ou non, je vois vraiment pas comment tu va pouvoir retrouver quoi que ce soit dans l'ordre des sommets.
Pour moi, c'est un peu comme si tu demandait dans quel ordre tu as rangé les entiers de 1 à 10 en donnant comme seule information "il est possible qu'ils ne soient pas dans l'ordre" : ç'est un peu "short" comme info...
P.S. En plus, un polygône "non connexe", je suis pas sûr que ça ait bien du sens ce truc là : si c'est pas connexe, c'est que tu as plusieurs polygône...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Merci por votre intétrêt et votre aide
Ben314 a écrit:Salut,
Y'a un truc qui m'échape : si ton polygone peut être connexe ou non, je vois vraiment pas comment tu va pouvoir retrouver quoi que ce soit dans l'ordre des sommets.
Pour moi, c'est un peu comme si tu demandait dans quel ordre tu as rangé les entiers de 1 à 10 en donnant comme seule information "il est possible qu'ils ne soient pas dans l'ordre" : ç'est un peu "short" comme info...
P.S. En plus, un polygône "non connexe", je suis pas sûr que ça ait bien du sens ce truc là : si c'est pas connexe, c'est que tu as plusieurs polygône...
J'ai mal exprimé en effet mon problème, j'ai n points sur un plan, je veux une méthode qui permette de relier ces n points par des segments avec les contraintes sivantes:
1°) aucun segment ne se coupe avec un autre
2°) et pour un point quelconque, il n' a que deux segments issus de ce point (ni un de plus ni un de moins). Visuellement et humainement, on sait le faire quand on voit les points sur le plan. Mais quel algorithme informatique peut être mis en oeuvre pour qu'un ordinateur puisse trouver au moins une solution voire toutes ? Merci
Je pense (à vérifier...) qu'il suffit de prendre un point bien choisi O (l'isobarycentre des points doit faire l'affaire) puis de trier les points Mi en fonction de l'angle ( Ox, OMi ) mesuré de 0 à 2pi à l'aide d'un quelconque algorithme de tri et on aura UNE des solutions (il me semble plus que probable qu'il y ait en général plusieurs solutions...)
En plus, le polygône obtenu sera "étoilé" (pour ceux qui savent ce que ça veut dire...)
Je laisse les férus d'info faire les tests... :zen:
En plus, le polygône obtenu sera "étoilé" (pour ceux qui savent ce que ça veut dire...)
Je laisse les férus d'info faire les tests... :zen:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
voici un exemple avec 2opt
Et avec la methode de Ben
Horrible les angles, perdu deux heures avec l'arctangente è_é. J'ai toujours pas compris pourquoi
atan(x) différait de atan2(y,x) mais bon, le ventre remporte le combat..
- Code: Tout sélectionner
[961,964],
[120,802],
[541,978],
[10,923],
[17,616],
[584,933],
[405,424],
[710,803],
[590,410],
[203,592]
function d(a,b){
return Math.sqrt(Math.pow(a[0]-b[0], 2)+Math.pow(a[1]-b[1], 2));
}
//remove crossing segments
function twoOpt(tour){
function updateTour(tour, i1, j1){
var cities=tour.slice(0);
var first=tour.slice(0, i1);
var last = tour.slice(j1);
var ji1=tour.slice(i1, j1).reverse();
var newT = first.concat(ji1).concat(last);
return newT;
}
var better = false;
var t=tour;
var newT=t;
for(var j=1; jd(t[j], t[i1])+ d(t[0], t[j1])){
var cities=t.slice(0);
var newT = cities.slice(0, j1);
newT=newT.concat(cities.slice(j1, i1+1).reverse());
better=true;
}
}
for(var i=0; i
//only useful for printing.
function gMap(canvas,op){
var ctx = canvas.getContext('2d');
function scale(cities){
var xs=cities.map(x=>x[0]), ys=cities.map(x=>x[1]);
var xmin=Math.min.apply(null, xs), xmax=Math.max.apply(null, xs);
var ymin=Math.min.apply(null, ys), ymax=Math.max.apply(null, ys);
return cities.map((city)=>[(city[0]-xmin)/xmax*300, (city[1]-ymin)/ymax*300]);
}
return {
draw:function(cities){
cities=scale(cities);
ctx.clearRect(0,0,canvas.width,canvas.height);
ctx.beginPath();
var [x,y]=cities.slice(-1)[0];
cities.forEach(function(city){
ctx.moveTo(x,y);
[x,y] = city;
ctx.lineTo(x, y);
ctx.stroke();
});
ctx.stroke();
ctx.closePath();
}
}
}
function getPolygone(cities){
var nbTries=0;
var res={tour:cities,better:true};
while(res.better &&nbTries
//main.js
function oneTag(t){return document.getElementsByTagName(t)};
var mapRef=gMap(oneTag('canvas')[0]);
var map=gMap(oneTag('canvas')[1]);
window.onload=function(){
oneTag('form')[0].onsubmit=function(e){
try{
var cities=JSON.parse('['+this.citiesLocation.value+']');
mapRef.draw(cities);
var sortedCities=getPolygone(cities);
map.draw(sortedCities);
}catch(e){
console.log(e);
}
e.preventDefault();
return false;
}
}
Et avec la methode de Ben
- Code: Tout sélectionner
[15,361],
[272,295],
[55,16],
[971,79],
[653,919],
[842,659],
[143,46],
[343,708],
[314,202],
[391,213]
function getAngle(A,B,O){
var [ux,uy]=[A[0]-O[0],A[1]-O[1]];
var [rx,ry]=[B[0]-O[0],B[1]-O[1]];
return Math.atan2(uy*rx-ux*ry,ux*rx+uy*ry);
}
function Ben314(tour){
tour=tour.map(x=>[+x[0],+x[1]]);
var res=tour.reduce((a,b)=>{return [a[0]+b[0], a[1]+b[1]]});
var barycenter=[res[0]/tour.length, res[1]/tour.length];
var t=tour[0];
return tour.map(x=>{
return {x:x,angle:getAngle(x,t,barycenter)}
}).sort((a,b)=>a.angle-b.angle).map(x=>x.x);
}
//only useful for printing.
function scale(cities){
var xs=cities.map(x=>x[0]), ys=cities.map(x=>x[1]);
var xmin=Math.min.apply(null, xs), xmax=Math.max.apply(null, xs);
var ymin=Math.min.apply(null, ys), ymax=Math.max.apply(null, ys);
return cities.map((city)=>[(city[0]-xmin)/xmax*300, (city[1]-ymin)/ymax*300]);
}
function gMap(canvas,op){
var ctx = canvas.getContext('2d');
return {
draw:function(cities){
cities=scale(cities);
ctx.clearRect(0,0,canvas.width,canvas.height);
ctx.beginPath();
var [x,y]=cities.slice(-1)[0];
cities.forEach(function(city){
ctx.moveTo(x,y);
[x,y] = city;
ctx.lineTo(x, y);
ctx.stroke();
});
ctx.stroke();
ctx.closePath();
}
}
}
function getPolygone(cities){
return Ben314(cities);
}
//main.js
function oneTag(t){return document.getElementsByTagName(t)};
var mapRef=gMap(oneTag('canvas')[0]);
var map=gMap(oneTag('canvas')[1]);
window.onload=function(){
oneTag('form')[0].onsubmit=function(e){
try{
var cities=scale(JSON.parse('['+this.citiesLocation.value+']'));
mapRef.draw(cities);
var sortedCities=getPolygone(cities);
map.draw(sortedCities);
}catch(e){
console.log(e);
}
e.preventDefault();
return false;
}
}
Horrible les angles, perdu deux heures avec l'arctangente è_é. J'ai toujours pas compris pourquoi
atan(x) différait de atan2(y,x) mais bon, le ventre remporte le combat..
la vie est une fête 
Sinon, pour "classer" les points par angle, tu peut éviter de calculer l'angle (donc éviter la fonction arctangente) en utilisant le fait que, si 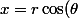) et
et 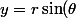) alors
alors =\frac{y}{x+\sqrt{x^2+y^2}) (qui en fait vaut
(qui en fait vaut  si tu as normalisé tes vecteurs) et classer par rapport à
si tu as normalisé tes vecteurs) et classer par rapport à  , c'est pareil que de classer par rapport à
, c'est pareil que de classer par rapport à ) .
.
Le seul problème, c'est si et
et 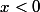 où
où  et
et =\pm\infty) ...
...
Le seul problème, c'est si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
coolos la comparaison avec y/(1+x)!!!
Au revoir l'arctangente et les prises de tete modulo pi
d'apres ton égalité au dessus,
vu que x=rcos(theta) et y=rsin(theta)
si on norme, on a pour y=0, x=+-1
comme de toute facon on compte de -pi à pi, c'est juste que le point il est soit au début, soit à la fin de la liste de points.
Comme c'est un polygone, ca change rien!
Au revoir l'arctangente et les prises de tete modulo pi
Le seul problème, c'est sioù
et
...
d'apres ton égalité au dessus,
vu que x=rcos(theta) et y=rsin(theta)
si on norme, on a pour y=0, x=+-1
comme de toute facon on compte de -pi à pi, c'est juste que le point il est soit au début, soit à la fin de la liste de points.
Comme c'est un polygone, ca change rien!
la vie est une fête 
bon en fait, si ca change un peu

L'algo que je mets en place c'est
soit un point O (le barycentre)
soit un point A.
Je considère le repère (O,i,j) orthonormé.
J'exprime mon point A en A' dans ce nouveau repère.
Donc A'=A+O
Et je calcule
Mais vraisemblablement, les deux points extremes ont décidé de tout couper
edit: il fallait faire une soustraction :mur:
A'=A-O


L'algo que je mets en place c'est
soit un point O (le barycentre)
soit un point A.
Je considère le repère (O,i,j) orthonormé.
J'exprime mon point A en A' dans ce nouveau repère.
Donc A'=A+O
Et je calcule
tan(theta/2)=A'_y/(A'_x+sqrt(A.A))
Mais vraisemblablement, les deux points extremes ont décidé de tout couper
edit: il fallait faire une soustraction :mur:
A'=A-O

la vie est une fête 
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

