Binome de newton
Discussion générale entre passionnés et amateurs de mathématiques sur des sujets mathématiques variés
-
djams2014
- Messages: 1
- Enregistré le: 22 Fév 2014, 18:25
-
 par djams2014 » 22 Fév 2014, 18:50
par djams2014 » 22 Fév 2014, 18:50
BJR
Pouvez m'aider SVP
Question : montrer que 3^(2n+1) + 2^(4n+2) est multiple de 7
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 22 Fév 2014, 19:01
par L.A. » 22 Fév 2014, 19:01
Bonjour.
Je pense pas qu'il faut utiliser le binôme, il faut plutôt passer par les congruences.
Commence par montrer que 3 + 2^2 = 0 [7] et 3^2 = 2^4 [7].
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 22 Fév 2014, 19:15
par jlb » 22 Fév 2014, 19:15
2^(4n+2)=4^(2n+1) et après tu utilises la formule de factorisation d'une somme de puissance ( Wikipédia identités remarquables, différence de puissances)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Fév 2014, 19:55
par Joker62 » 22 Fév 2014, 19:55
Hello,
Sinon une récurrence marche pas mal logiquement.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 23 Fév 2014, 15:20
par Ben314 » 23 Fév 2014, 15:20
Il me semble que le plus simple, c'est de terminer en utilisant le fait que

qui implique que :
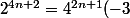^{2n+1}=-3^{2n+1}\ [7])
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
