Primitive
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
omalley76
- Messages: 9
- Enregistré le: 02 Mar 2008, 19:17
-
 par omalley76 » 20 Fév 2014, 14:56
par omalley76 » 20 Fév 2014, 14:56
Bonjour
Voilà je voudrais trouver une primitive de la fonction qui, à x, associe
/sqrt{x})
.
Par une IPP, je trouve une autre intégrale, celle de la fonction
)
et là... je sèche ... J'ai envisagé un changement de variables en posant
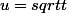
mais après, je me retrouve avec la fonction suivante :
)
...
Auriez-vous une idée ?
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 20 Fév 2014, 15:19
par Tiruxa » 20 Fév 2014, 15:19
omalley76 a écrit:Bonjour
Voilà je voudrais trouver une primitive de la fonction qui, à x, associe
/sqrt{x})
.
Par une IPP, je trouve une autre intégrale, celle de la fonction
)
et là... je sèche ... J'ai envisagé un changement de variables en posant
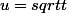
mais après, je me retrouve avec la fonction suivante :
)
...
Auriez-vous une idée ?
Bonjour :
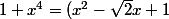(x^2+\sqrt{2}x+1))
Puis décomposer en éléments simples.
-
omalley76
- Messages: 9
- Enregistré le: 02 Mar 2008, 19:17
-
 par omalley76 » 20 Fév 2014, 15:42
par omalley76 » 20 Fév 2014, 15:42
Tiruxa a écrit:Bonjour :
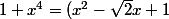(x^2+\sqrt{2}x+1))
Puis décomposer en éléments simples.
Merci beaucoup, j'y vois plus clair !
-
mobi
- Messages: 7
- Enregistré le: 18 Fév 2014, 10:32
-
 par mobi » 22 Fév 2014, 08:17
par mobi » 22 Fév 2014, 08:17
bonjour je dois trouver la primitive de (2x+1)/(x^2+1)^2.
QQun pourrait me mettre sur la voie svp..
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 22 Fév 2014, 08:24
par fibonacci » 22 Fév 2014, 08:24
mobi a écrit:bonjour je dois trouver la primitive de (2x+1)/(x^2+1)^2.
QQun pourrait me mettre sur la voie svp..
c'est de la forme

,
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 22 Fév 2014, 09:43
par fibonacci » 22 Fév 2014, 09:43
bonjour;
^2 }}} dx = \quad \left\{ \begin{array}{l}<br /> x = \tan t \\ <br /> dx = 1 + \tan ^2 tdt \\ <br /> \end{array} \right. \\ <br /> \int {\frac{{2x + 1}}{{(x^2 + 1)^2 }}} dx = \int {\frac{{2\tan t + 1}}{{(1 + \tan ^2 t)^2 }}} \cdot (1 + \tan ^2 t)dt \\ <br /> \end{array})
-
mobi
- Messages: 7
- Enregistré le: 18 Fév 2014, 10:32
-
 par mobi » 22 Fév 2014, 10:57
par mobi » 22 Fév 2014, 10:57
fibonacci a écrit:bonjour;
^2 }}} dx = \quad \left\{ \begin{array}{l}<br /> x = \tan t \\ <br /> dx = 1 + \tan ^2 tdt \\ <br /> \end{array} \right. \\ <br /> \int {\frac{{2x + 1}}{{(x^2 + 1)^2 }}} dx = \int {\frac{{2\tan t + 1}}{{(1 + \tan ^2 t)^2 }}} \cdot (1 + \tan ^2 t)dt \\ <br /> \end{array})
Merci , tres malin.....
-
mobi
- Messages: 7
- Enregistré le: 18 Fév 2014, 10:32
-
 par mobi » 22 Fév 2014, 13:56
par mobi » 22 Fév 2014, 13:56
mobi a écrit:Merci , tres malin.....
pourrais tu m'aider un peu 'plus je suis bloqué..stp.
-
Black Jack
 par Black Jack » 22 Fév 2014, 14:57
par Black Jack » 22 Fév 2014, 14:57
(2x+1)/(x²+1)² = 2x/(x²+1)² + 1/(x²+1)²
S (2x+1)/(x²+1)² = -1/(x²+1) + S dx/(x²+1)²
****
S dx/(x²+1)²
Poser x = tg(t)
dx = dt/cos²(t)
S dx/(x²+1)² = S (dt/cos²(t)) * cos^4t = S cos²(t) dt = (1/2). S (1 + cos(2t)) dt = t/2 + sin(2t)/4
***
S (2x+1)/(x²+1)² = -1/(x²+1) + (1/2).arctg(x) + (1/4).sin(2.arctg(x))
S (2x+1)/(x²+1)² = -1/(x²+1) + (1/2).arctg(x) + x/(2(x²+1))
:zen:
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 22 Fév 2014, 14:59
par Tiruxa » 22 Fév 2014, 14:59
sin(2t) =

-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 22 Fév 2014, 15:31
par fibonacci » 22 Fév 2014, 15:31
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
.
et là... je sèche ... J'ai envisagé un changement de variables en posant
mais après, je me retrouve avec la fonction suivante :
...