Dm de math, besoin d'aide svp sur les conditions d'existence, valeurs interdites...

par **Flora1223** » 10 Sep 2006, 10:44

Bonjour, je voudrais de l'aide pour quelques exercices qui me prennent la tete!
Il faut factoriser au maximum :
F(x)=(2x+3)² - (5x-1)²
et G(x)=(x-1)(x+2)²+(x²-1)(x+2)
Je crois que j'ai la bonne reponse, mais je suis pas sure je voudrais verifier. Merci!

Dans l'autre exercice, c'est ecrit simplifier, si possible, les expressions suivantes, apres avoir indiqué leur condition d'existence : (si quelqu'un pouV m'indiquer ce que cela veut dire svp)
a) (2x²+x)/x
b) [(2x-3)(x+1)]/ (2x²-3x)
c) (x²-4x)/[(x-1)²-1]
Quelqu'un peut m'aider, car j'ai beau chercher je ne trouve pas ce qu'est la condition d'existence!

Réduire au meme denominateur et ecrire sous la forme d'un quotient en précisant les valeurs interdites :
a) A(x)=[(4x-1)/(2x+1)]-[2x/(x-3)]
b) B(x)=[1/x]+[(x+1)/(x(x-2))]
c) C(x)=[1/(x(x+1))]-[1/(x²-1)]
Quelqu'un pourrait m'expliquer comment calculer les valeurs interdites, car maintenant j'ai un doute!
Veuillez m'aidez svp, merci d'avance!
J'ai besoin d'aide, merci de votre comprehension!

par **haydenstrauss** » 10 Sep 2006, 10:46

Flora1223 a écrit:Bonjour, je voudrais de l'aide pour quelques exercices qui me prennent la tete!
Il faut factoriser au maximum :
F(x)=(2x+3)² - (5x-1)²
et G(x)=(x-1)(x+2)²+(x²-1)(x+2)
Je crois que j'ai la bonne reponse, mais je suis pas sure je voudrais verifier. Merci!
!

Tu as fait quoi on va te dire si c'est bon ou pas

par **Flora1223** » 10 Sep 2006, 10:54

Alors!
Pour F(x), j'ai trouve (7x+2) (-3x+4)
et pour G(x) = (x-1)(x+2) (2x-1)
Est ce juste?
Merci d'avance!

par **nada-top** » 10 Sep 2006, 11:04

pour F(x) c bon :++: mais pour G(x) t'as fait une petite erreur :
G(x) = (x-1)(x+2)²+(x²-1)(x+2) = (x-1)(x+2) [(x+2) + (x+1) ] =...

2° c'est quoi une condition d'existence ? ..donc par ex pour la a) :

pour que ce quotient existe il faut que le dénominateur soit différent de 0 donc

est la condition d'existence , maintenant tu peux simplifier :

fais pareil pour les autre ...

par **Flora1223** » 10 Sep 2006, 11:16

Merci pour votre reponse, mais je comprends toujours pas pour le G(x)
Pourquoi (x-1)(x+2) [(x+2)+(x+1)]?
Peut-tu me marquer ton raisonnement en entier stp?

Et sinon pour la condition d'existence, est-ce comme la(es) valeur(s) interdite(s)??
Merci d'avance

par **nada-top** » 10 Sep 2006, 11:23

G(x) = (x-1)(x+2)²+(x²-1)(x+2) = (x-1)(x+2) (x+2) + (x+1)(x-1)(x+2) = (x+2)(x-1) [(x+2) +(x+1)]=...

Et sinon pour la condition d'existence, est-ce comme la(es) valeur(s) interdite(s)??

pour trouver la(es) valeur(s) interdite(s) tu raisonne de la meme manière par ex pour la a) la condition d'existence c'est :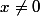

donc la valeur interdite c'est 0 .

par **Flora1223** » 10 Sep 2006, 11:32

Donc pour la b) C:
On cherche les x qui annulent (2x²-3x).
Ensuite on tente de résoudre l'équation 2x²-3x = 0
2x²-3x = 0
x(2x-3) = 0
donc x=0 ou x=3/2

et pour la c)
Je trouve x=2 ou x=0
Mes resultats sont-ils justes?

par **nada-top** » 10 Sep 2006, 11:37

oui c bien ça :happy2:
maintenant essaie de simplififer la b ) pour

et c) pour

par **Flora1223** » 10 Sep 2006, 11:49

Simplification de la b): il faut la factoriser non?
et pour la c) pareil non? il faut factoriser le denominateur et le numerateur non?
PS : Merci de m'avoir beaucoup aide deja!

par **nada-top** » 10 Sep 2006, 11:53

oui il faut factoriser et simplifier , et dis moi ce que tu trouves

par **Flora1223** » 10 Sep 2006, 12:34

Pour b), je trouve
(x+1)/(2x-3) est ce juste?
Pour c), je trouve
c) (x²-4x)/[(x-1)²-1]
=(x-2x)²/(x-1)²-1²
Mes resultats sont-ils justes?

Sinon pour les conditions d'existence (oui je sais encore), comment dois-je presenter??

par **nada-top** » 10 Sep 2006, 12:45

Pour b), je trouve
(x+1)/(2x-3) est ce juste?
Pour c), je trouve
c) (x²-4x)/[(x-1)²-1]
=(x-2x)²/(x-1)²-1²
Mes resultats sont-ils justes?

comment t'as trouvé ça? tu a du faire des erreurs ..

B° pour

(la condition d'éxistence) :

C° remarque que

est l'identidé remarquable

donc

continue..

par **Flora1223** » 10 Sep 2006, 12:59

ah oui dsl je sais pas ou j'avais la tete, dsl pour mon etourdissement!
alors pour a) je trouve 2x+1
pour b) je trouve [(2x-3)(x+1)]/[x(2x-3)] = (x+1)/x
pour c) je trouve [x²-4x]/[(x-2)x] = [(x-4)x]/[(x-2)]x
= (x-4)/(x-2)

Est ce juste maintenant?
PS : Pouvez vous m'expliquez comment presentez les conditions d'existence avant le calcul? C'est la meme presentation que les valeurs interdites ou pas?
Merci d'avance

par **nada-top** » 10 Sep 2006, 13:12

oui c'est ça et tu peux meme écrire

et c)

---
la condition d'existence pour la b) c'est

c-a-d x appartient à R privé des deux valeurs interdites

et 0 .
pareil pour c ..

3)les valeurs interdites de x sont les valeurs qui annulent le dénominateur .

par **Flora1223** » 10 Sep 2006, 13:24

Alors pour mon autre exercice,
a) A(x)= [(4x-1)/(2x+1)]-[2x/(x-3)]
v.i = 2x+1=0 ou x-3=0
x=-1/2 ou x=3
D=R\{-1/2 ; 3}

b) B(x)=[1/x]+[(x+1)/(x(x-2))]
v.i = x=0 ou x=?? je trouve pas puisqu'il y a x² ??
D=R\{0 ; ??}

c) C(x)=[1/(x(x+1))]-[1/(x²-1)]
v.i = x(x+1)=0 ou x²-1=0
x=?? meme probleme que le b) ?? ou x=1 ou x=-1
D=R\{?? ; 1 ; -1}
Est-ce juste???

par **nada-top** » 10 Sep 2006, 13:37

c bien pour a) donc tu en déduis que les valeurs interdites sont -1/2 et 3

pour b)

et

donc

et

---

et

-- les valeurs interdites sont 0 et 2 .

pareil pour c) (remarque :

)

par **Flora1223** » 10 Sep 2006, 13:54

Merci beaucoup pour votre aide!
Il me reste plus qu'a simplifier maintenant!
Merci encore et a bientot peut etre!
Flora

par **nada-top** » 10 Sep 2006, 13:54

de rien :happy2:

bon courage

Dm de math, besoin d'aide svp sur les conditions d'existence, valeurs interdites...

Dm de math, besoin d'aide svp sur les conditions d'existence, valeurs interdites...

Qui est en ligne