Bonjour,
Est ce que quelqu'un sait résoudre une equation différentielle d'ordre 2 avec second membre non continu ?
En particulier: sur ]0;1[
-y''+y=f(x)
où f(x) = 0 sur ]0;1/2[, 1 sinon
Merci beaucoup
Sacha
Equation différentielle d'ordre 2 avec second membre non continu
5 messages
- Page 1 sur 1
Salut,
Tout le problème dans un exercice de ce type est de savoir quelle régularité tu demande pour y aux points où f est discontinu...
Sans aucune info de plus, en considérant que l'on ne demande RIEN à la fonction y aux points 0 et 1/2, j'écrirais que :
1) L'équation -y''+y=0 sur un intervalle I a pour solutions y(t)=a.exp(t)+b.exp(-t) où a et b sont deux constantes arbitraires.
2) L'équation -y''+y=1 sur un intervalle I a pour solutions y(t)=1+c.exp(t)+d.exp(-t) où c et d sont deux constantes arbitraires.
DONC les solutions de ton équa-diff sont les fonction :=\left\{\matrix{<br />a.\exp(t)+b.\exp(-t)\ \ \ \ \ & \text{si } t\frac{1}{2}\ \ \ \ \right.)
où a,b,c,d,e,f sont des constantes arbitraires.
Aprés, si tu désire que y soit continue (voire dérivable) en 0 et en 1/2, ça te rajoute des conditions sur a,b,c,d,e,f.
Par contre il est clair au vu de l'équation différentielle de départ que tu ne peut pas avoir y deux fois dérivable en 0 et en 1/2.
Par exemple, si on part de y(t)=0 pour t<0 (c'est à dire de a=b=0), la continuité en 0 signifie que 1+c+d=0 et la dérivabilité en 0 que 1+c-d=0 donc que c=-1 et d=0.
Idem pour la continuité et la dérivabilité en 1/2 qui vont ensuite imposer que=d.\exp(\frac{1}{2})+e.\exp(-\frac{1}{2})\) et
et =d.\exp(\frac{1}{2})-e.\exp(-\frac{1}{2})\) c'est à dire
c'est à dire 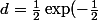-1\) et
et 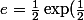) .
.
Tout le problème dans un exercice de ce type est de savoir quelle régularité tu demande pour y aux points où f est discontinu...
Sans aucune info de plus, en considérant que l'on ne demande RIEN à la fonction y aux points 0 et 1/2, j'écrirais que :
1) L'équation -y''+y=0 sur un intervalle I a pour solutions y(t)=a.exp(t)+b.exp(-t) où a et b sont deux constantes arbitraires.
2) L'équation -y''+y=1 sur un intervalle I a pour solutions y(t)=1+c.exp(t)+d.exp(-t) où c et d sont deux constantes arbitraires.
DONC les solutions de ton équa-diff sont les fonction :
où a,b,c,d,e,f sont des constantes arbitraires.
Aprés, si tu désire que y soit continue (voire dérivable) en 0 et en 1/2, ça te rajoute des conditions sur a,b,c,d,e,f.
Par contre il est clair au vu de l'équation différentielle de départ que tu ne peut pas avoir y deux fois dérivable en 0 et en 1/2.
Par exemple, si on part de y(t)=0 pour t<0 (c'est à dire de a=b=0), la continuité en 0 signifie que 1+c+d=0 et la dérivabilité en 0 que 1+c-d=0 donc que c=-1 et d=0.
Idem pour la continuité et la dérivabilité en 1/2 qui vont ensuite imposer que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
