Etude de fonction trigonometrique

[georg_21]

Bonjour,

J'etais en train de regarder cette vidéo http://www.youtube.com/watch?v=yZJ2QGhL8HI concernant les dérivées trigonométriques.. On trouve pour simplifier l'écriture elle fait (je suis d'accord) mais on aurait pas pû aussi faire car = sin(2x) ? Mais alors sin2x n'annule en car 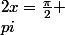et ça donne plus le même tableau de signe.. Pouvez-vous m'aider ?? Merci beaucoup :lol3:

[annick]

Bonjour,
tu as écrit :

f'(x)=sin2x, mais tu as oublié le - devant car -2sin2x+sin2x=-sin2x

Or, -sin2x=sin(-2x)

[siger]

Bonjour,

J'etais en train de regarder cette vidéo http://www.youtube.com/watch?v=yZJ2QGhL8HI concernant les dérivées trigonométriques.. On trouve pour simplifier l'écriture elle fait (je suis d'accord) mais on aurait pas pû aussi faire car = sin(2x) ? Mais alors sin2x n'annule en car et ça donne plus le même tableau de signe.. Pouvez-vous m'aider ?? Merci beaucoup :lol3:

bonjour,

1- sin(2x) ne s'annule pas pour 2x= pi/2 !!!!!!'n
2- -sin(2x) est toujors negatif pour x compris entre 0 et pi/2 ( domaine envisagé)

[georg_21]

Bonjour,
tu as écrit :

f'(x)=sin2x, mais tu as oublié le - devant car -2sin2x+sin2x=-sin2x

Or, -sin2x=sin(-2x)

Merci beaucoup.
Par contre, elle étudie le signe et moi j;'aurais etudié le signe de ce qui revient au même mais si je cherche les zeros de c'est en pi/4 +k pi non ? Sinon comment je fais pour les trouver sans développer l'expression sin2x ?Merci beaucoup.

[annick]

sin(2x)=0=sin(kpi)

2x=kpi

x=kpi/2

Edit: corrigé à la suite de la remarque de Siger qui était fort juste (l'effet du dimanche, c'est pour moi !!! :lol3: )

[siger]

Re

j'ai un probleme .... (est-ce que c'est un effet du dimanche?)
le zero de sin(2x) n'a jamais ete pi/4 + k*pi........

sin(2x) =0 conduit a 2x = k*pi
d'ou x= 0 et x= pi/2

ce sont les même zeros que sinx*cosx , non?

[georg_21]

OUIIII. (Effet du dimanche soir..)
Je viens de m'en rendre compte il y a une petite demi heure... J'ai eu peur pendant un certain temps :P Merci bien !