bousoir à tous,
je cherche à resoudre l'équation fonctionnelle suivante :
f(X-R) = Cte*f(X)
cte : contante de valeur fixé, reelle ou complexe.
f fonction continue et derivable de : RxRxR ----> C
X est un vecteur (x,y,z) variable
R est aussi un vecteur, mais un vecteur de valeur fixée.
j'ai trouvé pour l'instant 2 types de solutions :
f= constante :ptdr:
et
f(X) = constante*exp(i*K*X) :hein:
K etant un vecteur fixé et X le vecteur (x,y,z)...
mais je n'arrive pas à trouver d'autres solutions ou bien à montrer que ce sont les seules solutions... :briques:
si quelqu'un peut m'aider .... :zen:
merci
Equation fonctionnelle
3 messages
- Page 1 sur 1
Suppose que 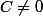 . Je te donne une idée: essayer de contruire une fonction de période
. Je te donne une idée: essayer de contruire une fonction de période  . Tu as:
. Tu as:
=Cf(X)) , l'astuce est profiter de quelque fonction
, l'astuce est profiter de quelque fonction  connue telle que
connue telle que =h(X)f(X)) soit périodique.
soit périodique. f(X)=g(X)=g(X-R)=h(X-R)f(X-R)=Ch(X-R)f(X)) . il est désirable que
. il est désirable que =\frac{1}{C}h(X)) (*). Tu as déjà donné une fonction qui peut nous aider:
(*). Tu as déjà donné une fonction qui peut nous aider: =Ae^{\langle K,X\rangle}) . Remplaçant en (*) et pensant au cas
. Remplaçant en (*) et pensant au cas 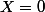 tu pourras obtenir valeurs pour
tu pourras obtenir valeurs pour  et
et  . Il faut que tu continues avec les calculs et les détails. J'aimerais bien savoir si tu as bien terminé l'exercice.
. Il faut que tu continues avec les calculs et les détails. J'aimerais bien savoir si tu as bien terminé l'exercice.
jose_latino a écrit:Suppose que. Je te donne une idée: essayer de contruire une fonction de période
. Tu as:
, l'astuce est profiter de quelque fonction
connue telle que
soit périodique.
. il est désirable que
(*). Tu as déjà donné une fonction qui peut nous aider:
. Remplaçant en (*) et pensant au cas
tu pourras obtenir valeurs pour
et
. Il faut que tu continues avec les calculs et les détails. J'aimerais bien savoir si tu as bien terminé l'exercice.
merci de tes infos, josé, je vais m'y attacher. Nota : ceci n'est pas un exercice, c'est un element de demonstration que j'essaye de reconstituer car la demo du livre ne tient pas la route.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
