Borne superieur , inferieur

[Sisi75]

Bonjour , j ai un dm de maths mais j ai des difficultes a comprendre les demontration .

Voila mon exercice et ma recherche

Pour l ensemble suivant determiner la borne superieur, inferieur, maximum et minimum

F ={q€Q, (1+q)au carre<2}

voila ma recherche,

Quelque soit q appartenant a Q, (1+2) au caree<2, donc 2 est un majorant de F.

Montrons que 2 est le plus petit des majorants, ( equivaut a sup(f) =2)

Quelque soit E ( epsilon)>0, on a 1+E qui n est pas un majorant

Il existe x = (1+q) qui appartient a f qui est superieur a 2-E
Puisque 2 est un majorant de F on a aussi,
X<2

Donc x appartient [ 2-E, 2]

ce qui signifie que 2 est le plus petit des majorant

Merci de votre aide

[jonses]

Salut,


[quote="Sisi75"]


Pour l ensemble suivant determiner la borne superieur, inferieur, maximum et minimum

F ={q€Q, (1+q)au carre0, on a 1+E qui n est pas un majorant

Il existe x = (1+q) qui appartient a f qui est superieur a 2-E
Puisque 2 est un majorant de F on a aussi,
X0[/tex] et

ce qui montre que et cela étant valable pour tout

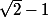Donc et sont respectivement un minorant et un majorant dans R de l'ensemble F.

Donc admet une borne sup et une borne inf dans R. Mais peut-être on demandait de déterminer une borne inf et une borne sup dans Q (ce qui n'est pas possible si je me trompe pas) ?

-maintenant si on note et respectivement la borne sup et la borne inf de l'ensemble, on peut montrer que et que en passant par l'absurde :

Si alors donc il existe un rationnel 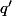tel que et vu que :

donc d'où ce qui veut dire que or ce qui n'est pas possible.

Pour le max et min je vois pas trop...

[Sisi75]

merci pour ton aide , j ai vraiment du ma l a comprendre ... j ai vu comment tu raisonne mais je ne comprend pas ,

la prof utilise la définition du cours , avec epsilon ... j ai essaye de suivre son raisonnement ... mais j ai du mal ...

l ensemble etudie s écrit F= { q E Q, /(1+q)^2<2)
ce qui ne revient pas a dire tout simplement que 2 est un majorant ?

la prof écrit " montrons que 2 est un majorant de F, sup(F) = 2

puis elle écrit quequesoit epsilon >0, chercher a = (1+q)^2 tq a>2-epsilon



en procedant de cette sorte je trouve [racine2-(1+q)][racine2+(1+q)]
mais je n arrive pas a conclure ....


ou je peux encore écrire (1+q)^2-2<0, donc 0 serait un majorant .....


je vais étudier ta proposition ce soir ...

merci a toi

[jonses]

merci pour ton aide , j ai vraiment du ma l a comprendre ... j ai vu comment tu raisonne mais je ne comprend pas ,

la prof utilise la définition du cours , avec epsilon ... j ai essaye de suivre son raisonnement ... mais j ai du mal ...

l ensemble etudie s écrit F= { q E Q, /(1+q)^20, chercher a = (1+q)^2 tq a>2-epsilon

J'ai moi aussi du mal à bien saisir le problème,


Si on suppose que sup(F)=2,

alors pour tout de F, et 2 est le plus petit majorant de F, donc ne majore pas F

donc on dispose de tel que

donc soit

donc or on devrait avoir ...


Là franchement je comprends plus... désolé

[mrif]

soit encore
Donc et sont respectivement un minorant et un majorant dans R de l'ensemble F.

Donc admet une borne sup et une borne inf dans R.

En partant de ton idée on peut écrire F sous une forme simple.
est équivalent à
Donc

On en déduit la borne inf et sup de F, et comme ces bornes ne sont pas dans F, celui-ci n'admet ni min ni max.

[Sisi75]

En partant de ton idée on peut écrire F sous une forme simple.
est équivalent à
Donc

On en déduit la borne inf et sup de F, et comme ces bornes ne sont pas dans F, celui-ci n'admet ni min ni max.

Merci de ton aide ... Le min et le max n existe pas car ce ne sont pas des rationnels car ils ne s ecrivent pas sous forme de fraction l donc n appartiennent pas a Q. C est bien cela?
Merci a tous les deux en tous cas , j essaye de faire la demonstration et je la poste , ca pourra toujours servir a quelqu un dans l avenir ....

[Sisi75]

Bonjour ,
voila comment j ai procède en m appuyant de vos remarques

F={q appartient Q, (1+q)^2 <2)}

l expression peut s écrire (1+q)^2 - 2 <0

ou encore ((1+q)-racine 2)((1+q)+racine 2) <0

on trouve des valeurs qui annulent q et on fait un tableau de signes .

cette expression est négative pour -rac2-1 < q< rac 2 -1

d apres la définition,
F admet une borne supérieure ssi
F existe et si F est majorée.

donc
F existe car si je prends 0, l expression est vérifié.
F est borne , donc majorée et minorée.

Donc il existe une borne supérieur et une borne inférieure.

Maintenant , il faut que je démontre que la borne supérieure ( reps borne inf) est le plus petits des majorants .

est ce que mon raisonnement tiens la route ?

merci encore pour vos explications ,

je tente de demontrer que ce sont les plus petits des majorants et je reviens vous le soumettre ... je sens que ça ne va pas être facile

Bonne journée