Vitesse angulaire : w

[mydoudouitsk]

Bonjour, j'ai trois petites questions qui me posent énormément de problème... Pourriez vous m'aider?

1-Comment peut-on déduire d'un mouvement circulaire que c'est un mouvement circulaire uniforme pour que w=0?

2-Et donc de même comment savoir si un mouvement circulaire n'est pas uniforme mais varié?

Mon cours me dit qu'un mouvement circulaire uniforme à un vecteur accélération différent du vecteur nul, donc pour moi la vitesse ne fait qu'augmenter (cf satellite).
Mais alors qu'est ce qu'un mouvement circulaire varié?

3-Qu'elle est la différence?

[Mathusalem]

Si tu dessines un vecteur vitesse V
A son bout, un vecteur acceleration A, orthogonal a V.

Alors, tu vois que A n'a pas d'influence dans la direction de V, mais seulement dans le sens Orthogonal.

Ainsi, une acceleration peut tout aussi bien servir a changer la direcion d'une vitesse que changer sa norme (change de direction = composante orthogonale a la direction / augmenter norme = composante parallele a la direction ).

Par exemple, dans une spirale, il y a un vecteur acceleration qui est legerement en oblique par rapport a la vitesse, de maniere a donner une composante orthogonale ET tangentielle.

[mydoudouitsk]

d'accord mais nous ne pouvons différencier le mouvement circulaire varié du mouvement circulaire uniforme qu'avec un schéma? Mais si il n'y a qu'un énoncé comment peut -on déduire du mouvement en question?
Je pense bien qu'une réponse généralisée ne pourrait être réellement donnée, auriez-vous dans ce cas des indices "types" qui montreraient la présence de ces mouvements?

[Mathusalem]

Essaye de formuler ta question plus clairement. Je ne sais pas ce qu'est ton problème

Peut etre lire cet article t'eclairera :

http://maths-forum.com/showthread.php?t=107964

[Mathusalem]

Peut etre que ceci t'aidera :

Pour qu'un mouvement soit parfaitement circulaire, il faut qu'a tous moments, l'acceleration centripete (Tangentielle pointant vers le centre) ait une norme de v^2 / r.

Ainsi, si v n'est pas constant mais croissant, alors l'acceleration centripete doit etre croissante pour maintenir un cercle. Autrement, elle est trop faible pour rabattre l'objet de vitesse v sur un chemin circulaire, et on part en spiral excentrique (qui croit vers dehors)

Tu peux donc avoir une vitesse tangentielle variable et un mouvement circulaire, pour autant que ton acc. centripete varie comme ta vitesse tangentielle au carré. Alors, on assiste a un mouvement circulaire variable.

[mydoudouitsk]

"Ainsi, si v n'est pas constant mais croissant, alors l'acceleration centripete doit etre croissante pour maintenir un cercle."

mais si v est croissant l'accélération peut être constante, non?
ou si l'accélération est une constante alors v aussi?

Et sinon un mouvement circulaire varié peut-être représenté par quelle forme géométrique dans un énoncé? Un cercle? ou ce cercle est uniquement réservé au mouvement circulaire uniforme?

Autre question ( en relation)

Si je prend la rotation de la Lune autour de la Terre peut on qualifier ce mouvement de mouvement circulaire uniforme ou varié?

[Mathusalem]

mais si v est croissant l'accélération peut être constante, non?
ou si l'accélération est une constante alors v aussi?

Oui, mais distingue bien les deux cas de figure ainsi que le propos tenu :

Dans une logique vectorielle, si l'acceleration est colineaire avec la vitesse, alors la norme de la vitesse augmente (par exemple de 3m/s a 5m/s selon x). Ici, l'acceleration constante donne une vitesse variable dans la norme

Si l'accélération est orthogonale avec la vitesse, alors la direction de la vitesse change (par exemple de 3m/s selon x a 3m/s selon y). Ici, la norme de la vitesse reste constante malgré le fait qu'il y ait une accélération, car celle-ci est orthogonale et n'influe que sur la direction de v.

On remarque par le calcul (voire preuve dans ton bouquin) que :
Afin qu'un objet vecteur vitesse v soit dévié de manière à ce que l'objet décrive un cercle, il faut qu'il y ait une accélération orthogonale à la vitesse de celui-ci, dont la norme est de
(1)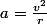 ou r est le rayon du cercle décrit.

Ainsi, on a une accélération de norme constante qui influe sur un vecteur de norme constante, mais les directions ne le sont pas !
Si la condition sous (1) est vérifiée, alors on assiste à un mouvement circulaire, caractérisé par un vecteur w de vitesse angulaire.

Or, la condition (1) n'oblige pas que la norme de tes vecteurs soit constante, elle te donne une relation entre les normes afin que l'objet en question soit sur un cercle. Ainsi, si la norme de la vitesse augmente par une accélération tangentielle d'un facteur 2, il faudra, pour garder un cercle, selon (1), une accélération orthogonale qui augmente d'un facteur 4.

Si la relation entre les normes de la vitesse et accélération orthogonale ne satisfait pas (1), alors tu auras un mouvement courbe, spiraloide concentrique/excentrique etc... Mais PAS un cercle !

Puisque v = w*r, et que le rayon du cercle reste constant, on assiste a un mouvement circulaire uniforme si la vitesse tangentielle est constante (norme), ce qui équivaut a dire que w est constante (dans la norme).

Si v n'est pas constante dans la norme, ET que l'accélération orthogonale change de manière à encore créer un mouvement circulaire, ALORS le mouvement circulaire est dit variable, caractérisé par un w de norme non constante.

Et sinon un mouvement circulaire varié peut-être représenté par quelle forme géométrique dans un énoncé? Un cercle? ou ce cercle est uniquement réservé au mouvement circulaire uniforme?

Donc après tout ça, tu auras compris que mouvement circulaire varié, ça dépend de la définition que tu as de "circulaire". C'est soit un mouvement sur un cercle ou la vitesse tangentielle est variable, soit un mouvement spiraloide ( dans lequel cas (1) n'est pas vérifié ).

En gros, pour savoir si ton mouvement circulaire varié est un cercle, il faut regarder si (1) est satisfait. S'il ne l'est pas, tu as tout, sauf un cercle.

Si après ça, ce n'est pas clair, il faudra franchement que je me creuse pour rendre cela plus intelligible