Benjamin631 a écrit:Oui, c'est juste.
comment à partir de la somme des forces, je peux montrer que l'équation du mouvement de l'électron s'écrit:
idée:
il faut que je remplace
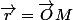
!!!
et là j'aurai une chance de me rapprocher de l'expression demandée??!
Benjamin631 a écrit:Oui, c'est juste.
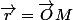
!!!
Benjamin631 a écrit:Tu les trouves par identification. Devant r et dr/dt, tu as des termes, fonction de k et m. Tu peux donc poser alpha=... et omega0=....
Devant r et dr/dt, tu as des termes, fonction de k et m.
nivéa a écrit:le PDF:
-kr -hv -eE =ma
pour me rapprocher de l'équation, je mets tout en fonction de r
donc,
-kr -h(dr)/(dt) -eE =m(d²r)/(dt²)
alors, je trouve:
(d²r)/(dt²) + kr+h(dr)/(dt) = ( -eE)/m
nivéa a écrit:qd, il demande de trouver l'expression de l'amplitude complexe:
ma réponse:
sachant, que le régime imposé est permanent, je suis en PFS
donc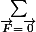
ici, le facteur d'amortissement est nul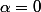
donc, on se trouve avec une expression de cette forme:
c'est une équation d'un oscillateur harmonique premier dimension.
J'écris ensuite, l'expression de l'amplitude :=A\cos(wt)+B\sin(wt))
on pose les conditions initiales:
1:=x_o)
2: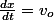
Soit
1:
1:
2:=-wA\sin(0)+wB\cos(0))
2:, d'ou
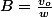
donc, l'expression de l'amplitude complexe est:
Est-ce que jusque là c'est bon?!!
nivéa a écrit:donc, E ici vaut: E(t)=Eo coswt ex.
Ensuite, tu appliques la transformation complexe, c'est-à-dire que la dérivation revient à multiplier par (j*w), et la double dérivation revient à multiplier par (j*w)²=-w². Tu n'as plus d'équation différentielle à résoudre, c'est bien là tout l'intérêt de la technique.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :