Temps d'effondrement d'un amas stellaire

[Sourire_banane]

Bonsoir,

Je veux donner une réponse à la question I)3)2- de ce sujet mais nulle part dedans je ne vois comment on peut déterminer la masse d'un atome d'hydrogène. En plus la calculatrice étant interdite, je me vois calculer un tel temps (où il y a des pi, des racines) au lieu de faire des estimations plutôt grossières. On la sort de son chapeau, la masse de l'hydrogène ?

http://www.sujets-de-concours.net/sujets/x/2009/pc/phys1.pdf

Merci.

[Skullkid]

Salut, comme la calculatrice est interdite on ne s'attend sans doute pas à des résultats très précis (genre tu dois t'en sortir avec grosso modo pi = 3, e = 2.7, sqrt(2) = 1.4 et sqrt(3) = 1.7). Pour la masse de l'hydrogène tu peux la sortir du nombre d'Avogadro, vu que tu sais que la masse molaire de l'hydrogène est 1 g/mol (pour un sujet de PC on doit aussi s'attendre à ce que tu connaisses les masses molaires de He, C, O et N).

[Sourire_banane]

Salut Skullkid,

Ah d'accord. Pour le carbone ça va puisque c'est de là que découle la déf du nombre d'Avogadro, mais pour les autres je sais pas encore...

Ok, pour la question 3- ça doit être hors-programme mais je parie que c'est à cause d'une force de pression ? Je saurais pas dire laquelle.

Ensuite il y a qqchose qui me pose pb dans la question I)4)2) : Pour la I)4)1 j'ai trouvé que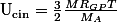 en reprenant la définition du modèle cinétique. Sauf qu'en faisant ainsi j'ai écrit que 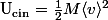et je suis pas trop sûr pour la masse !
Du coup dans la question I)4)2) j'ai développé mais je ne vois pas où on peut faire tendre R vers sa valeur limite !

[Skullkid]

Oui c'est les forces de pression qui vont contrer l'effondrement (normalement c'est pas hors programme, quand même, la statique des fluides !).

C'est bon pour la 1.4.1. Je n'ai pas trop compris la raison de ton doute. La façon la plus "fondamentale" de le voir à mon avis c'est de partir de l'équipartition (kT/2 par particule par degré de liberté, donc 3kT/2 par atome dans un gaz monoatomique donc etc). J'imagine que dans ton cas tu as raisonné à partir de la vitesse RMS sqrt(3kT/m), ça marche aussi.

Pour la 1.4.2. il s'agit de trouver la valeur de R0 pour laquelle Eg + 2Uc = 0. C'est une valeur critique, pas limite :o

[Sourire_banane]

Oui c'est les forces de pression qui vont contrer l'effondrement (normalement c'est pas hors programme, quand même, la statique des fluides !).

C'est bon pour la 1.4.1. Je n'ai pas trop compris la raison de ton doute. La façon la plus "fondamentale" de le voir à mon avis c'est de partir de l'équipartition (kT/2 par particule par degré de liberté, donc 3kT/2 par atome dans un gaz monoatomique donc etc). J'imagine que dans ton cas tu as raisonné à partir de la vitesse RMS sqrt(3kT/m), ça marche aussi.

Pour la 1.4.2. il s'agit de trouver la valeur de R0 pour laquelle Eg + 2Uc = 0. C'est une valeur critique, pas limite

Très exactement, j'étais parti de la vitesse quadratique moyenne. En fait je ne savais pas s'il fallait prendre la masse totale ou la masse d'une particule.

Oui oui valeur critique, autant pour moi :hum:

Je trouve une expression homogène pour le rayon critique, c'est rassurant.