Bon, alors je suis finalement parvenu à la réponse, pour ceux que ça intéresse.
Bon, la vitesse du point de contact

s'écrit comme suit :
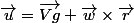
où Vg est la vitesse du centre de masse, w la rotation eventuelle, et r le rayon de la sphere.
En appliquant le théorème du centre de masse, on a que
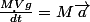
Ici, seule la friction agissant au point de contact agit comme force. Il n'y en a pas d'autre.
En dérivant
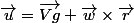
on obtient
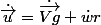
, car r ne varie pas en fonction du temps et
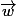
et
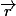
sont orthogonaux.
Par le théorème du moment cinétique, on sait que
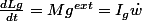
C'est à dire que la somme des moments de force (la somme n'apparait pas mais elle est implicite) est égale à l'accélération angulaire fois le moment d'inertie en ce point (j'ai choisis g).
Un moment de force par rapport à un point g est défini comme la distance orthogonale entre ce point et le point d'application de la force, fois cette force. En l'occurence, la seule force dans ce problème est la force de friction qui agit contre le sens de rotation et qui s'applique au point de contact(sans friction, elle ne pourrait pas rouler !). Par conséquent, vu du point G, le moment de force Mg est
Mg = rF = rMa = rMVg
On a donc par le th. du moment cinétique
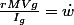
En substituant, on conclut donc
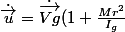)
EDIT: Pour un schéma : Dessinez un cercle, avec un point G au milieu, un point de contact A, et une force F de fricton partant de A dans le sens que vous désirez (en effet, dans quelle sens tourne la boule ? Choisissez!)
EDIT2: Aux puristes, je n'ai pas utilisé la notation vectorielle dans la dernière partie, je sais, alors qu'on ne vienne pas me dire
qu'on aura tout vu 
