Vie89 a écrit:Bonjour

,
Voici encore un exercice, dont je n'aurais pas la correction (exercice supplémentaire), donc je m'en remets à vous pour m'aiguiller, confirmer mon raisonnement, ...
Une tortue mutante de masse m est placée à l'extrémité d'une planche de longueur L et de masse [B]M, qui flotte à la surface de l'eau. A un instant précis, la tortue saute avec un angle

par rapport à la planche.
Calculez la vitesse Vo que la tortue doit prendre pour atterrir précisément à l'extrémité droite de la planche.[/B]
=====================================================================
Je ne sais pas combien de temps peut prendre la résolution de cet exercice, mais il me semble que c'est assez rapide, si quelqu'un se sent d'attaque, voici le résultat que j'ai trouvé :
Vo = }{g} + \frac{2m\sin (\alpha)}{g(M+m)} \ $)
Quelqu'un peut-il me confirmer ce résultat ? Si il y a d'autres idées, n'hésitez pas, je développerai mon raisonnement à ce moment là.
Merci d'avance pour votre aide

.

En négligeant ce qu'il se passe sur la verticale pour ce qu'il en est de la quantité de mouvement, je raisonnerais comme ceci :
La tortue fait un saut d'angle alpha et de vitesse v0 donc on peut calculer la distance à laquelle elle attérira :
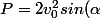cos(\alpha)\frac{1}{g})
De plus, la tortue est animée d'une vitesse horizontale
)
donc la planche, par conservation de quantité de mouvement possède une vitesse
)
Le temps que met la tortue pour faire un saut est 2 fois le temps qu'elle met pour monter, c'est-a-dire atteindre une vitesse nullle. Ainsi, le temps de saut est
}{g})
Il faut qu'a ce moment là, la planche ait précisément parcouru une distance L-P
L'équation du mouvement. La planche se déplaçant avec une vitesse de norme
)
, il suffit que
\frac{2v_0sin(\alpha)}{g} = L-P)
Ainsi, l'extrêmité droite de la planche se trouvera exactement là où la tortue attérit.
Tu te retrouves donc avec
gM}{2msin(\alpha)cos(\alpha))
J'ai rien vérifié. Remarque ma solution a la bonne dimension. La tienne n'est pas homogène en dimensions, donc tu sais tout de suite qu'elle est fausse


