Un peu de thermo...
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 17 Déc 2008, 15:49
par farator » 17 Déc 2008, 15:49
Salut,
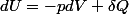
Soit pour un gaz parfait :
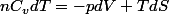
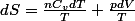
D'où
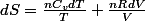
Flemme d'écrire les calculs...j'arrive à :
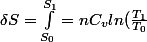+nR.ln(\frac{V_1}{V_0}))
On a le coefficient polytropique
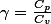
Si on prend une transformation adiabatique réversible :
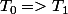
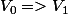
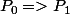
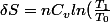+nR.ln(\frac{V_1}{V_0})=0)
=\frac{C_p}{R}ln(\frac{V_1}{V_0}))
J'ai trouvé la relation
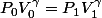
...Et je ne suis pas foutu de trouver une relation entre T1, V1, T0, V0 et

à partir de
=\frac{C_p}{R}ln(\frac{V_1}{V_0}))
:doh:
De même pour
-nR.ln(\frac{P_1}{P_0})=0)
Merci :we:

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 17 Déc 2008, 17:17
par fatal_error » 17 Déc 2008, 17:17
salut,
a tout hasard :
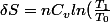+nR.ln(\frac{V_ 1}{V_0})=0\\<br />ln(\frac{T_1}{T_0})=\frac{R}{C_v}ln(\frac{V_0}{V_1})\\<br />\frac{T_1}{T_0}=(\frac{V_0}{V_1})^{\frac{R}{C_v}})
?
la vie est une fête

-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 17 Déc 2008, 17:25
par farator » 17 Déc 2008, 17:25
Salut

En fait je sais qu'il y a une relation :
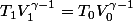
que je n'arrive pas à retrouver.
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 17 Déc 2008, 17:28
par XENSECP » 17 Déc 2008, 17:28
Loi de Laplace à partir de PV^a = cste :)
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 17 Déc 2008, 17:33
par farator » 17 Déc 2008, 17:33
Ui je viens de voir ça :id:
Mais comment la démontrer à partir de
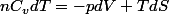
?

-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 17 Déc 2008, 17:38
par XENSECP » 17 Déc 2008, 17:38
on parle de gaz parfait :)
donc c'est pas vraiment nCv mais plutôt dU à déterminer ^^
mais on va pas te refaire tout le cours (enfin pas moi) !!!
Cherche sur google à la limite !
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 17 Déc 2008, 22:10
par farator » 17 Déc 2008, 22:10
Je demande pas qu'on me refasse le cours, puisqu'on n'a vu que la formule
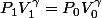
Je voudrais juste savoir comment passer de
=\frac{C_p}{R}ln(\frac{V_1}{V_0}))
à
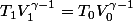
si c'est possible


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 17 Déc 2008, 23:03
par fatal_error » 17 Déc 2008, 23:03
allez, j'insiste encore au bonheure la chance.
Comme tout a l'heure avec le coup de l'exponentiel :
=\frac{C_p}{R}ln(\frac{V _1}{V_0})\\<br />ln(\frac{T_1}{T_0})=\frac{C_p}{R \gamma}ln(\frac{V _1}{V_0})\\<br />ln(\frac{T_1}{T_0})=\frac{ - C_p}{R \gamma}ln(\frac{V _0}{V_1})\\<br />\frac{T_1}{T_0}=(\frac{V _0}{V_1})^{\frac{ - C_p}{R \gamma}}\\)
Du coup, la on veut que
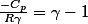
et a tous les coups, ya une formule avec C_p et C_v ou qqch dans ce gout la... :briques:
la vie est une fête

-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 17 Déc 2008, 23:31
par farator » 17 Déc 2008, 23:31
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités