Oscillateur Harmonique Quantique

par **Babe** » 31 Mar 2008, 18:18

Bonsoir,

j'ai fais un exo sur l'oscillateur harmonique quantique
pour le 1er niveau d'energie j'ai

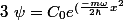et la il me demande à quoi sert C0 et quelle est son unité

alors pour l'unité, j'ai utilisé

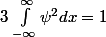
(avec une norme sur psi)

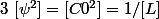
d'où

mais ca me parait bizarre...

sinon pour son utilité je vois pas trop, j'aurais repondu, "elle est la parce que la resolution de l'equation la fait apparaitre..." mais la qualité de cette interpretation tend vers 0...

merci de votre aide

par **Dominique Lefebvre** » 31 Mar 2008, 19:22

Babe a écrit:Bonsoir,

j'ai fais un exo sur l'oscillateur harmonique quantique
pour le 1er niveau d'energie j'ai

et la il me demande à quoi sert C0 et quelle est son unité

alors pour l'unité, j'ai utilisé (avec une norme sur psi)

d'où
mais ca me parait bizarre...

sinon pour son utilité je vois pas trop, j'aurais repondu, "elle est la parce que la resolution de l'equation la fait apparaitre..." mais la qualité de cette interpretation tend vers 0...

merci de votre aide

Bonsoir,
Ta condition de normalisation me semble très curieuse... Il me semble que C0 = (m*omega/pi*hbarre)^(1/4) ... Je n'ai pas fait l'équation aux dimensions mais je n'ai pas l'impression que cela donne L^(-1/2)

par **Babe** » 31 Mar 2008, 20:28

Rain' a écrit:Justement si

(m*omega/pi*hbarre)^(1/4) = ([M]*[T^-1]/[M]*[L²]*[T^-1] )^(1/4) = [L^-1/2]

j'ai téléchargé la correction que le prof a mis sur le net
pour l'unité c'est bien ca
Rain tu as raison, C0 sert bien à normer la fonction d'onde (je la trouve quand meme un peu dénué de sens cette question)

par **Dominique Lefebvre** » 31 Mar 2008, 20:53

Rain' a écrit:Justement si

(m*omega/pi*hbarre)^(1/4) = ([M]*[T^-1]/[M]*[L²]*[T^-1] )^(1/4) = [L^-1/2]

Ah bon... Je ne m'en souvenais plus!

par **Babe** » 31 Mar 2008, 21:09

Dominique Lefebvre a écrit:Ah bon... Je ne m'en souvenais plus!

même les plus grand ne peuvent pas toujours être à 100% !
je note quand même sur mon calepin: "31 mars 2008 petite défaillance de Domi, qui pourrait être vraisemblablement liée au changement d'heure :we: "

par **Dominique Lefebvre** » 31 Mar 2008, 21:35

Babe a écrit:même les plus grand ne peuvent pas toujours être à 100% !
je note quand même sur mon calepin: "31 mars 2008 petite défaillance de Domi, qui pourrait être vraisemblablement liée au changement d'heure :we: "

Oh non, aucune excuse... j'ai perdu l'habitude d'évaluer la dimension d'une expression. J'aurai du m'en souvenir... Mais bon, je me suis souvenu de l'expression de C0 et aussi de la condition de normalisation....

par **Babe** » 31 Mar 2008, 21:37

Dominique Lefebvre a écrit:Mais bon, je me suis souvenu de l'expression de C0 et aussi de la condition de normalisation....

oui je ne critique point, ce n'est qu'une petite plaisanterie d'un bébé physicien qui veut devenir grand lol

par **Dominique Lefebvre** » 31 Mar 2008, 21:41

Babe a écrit:oui je ne critique point, ce n'est qu'une petite plaisanterie d'un bébé physicien qui veut devenir grand lol

C'est fou ce qu'on oublie vite ce que l'on ne pratique pas!

par **Babe** » 31 Mar 2008, 21:45

Dominique Lefebvre a écrit:C'est fou ce qu'on oublie vite ce que l'on ne pratique pas!

oui et puis plus on connait de choses, plus on a de choses à oublier :triste:

par **Dominique Lefebvre** » 31 Mar 2008, 21:52

Babe a écrit:oui et puis plus on connait de choses, plus on a de choses à oublier :triste:

Absolument :ptdr: :ptdr: :ptdr: Et surtout tu t'aperçois qu'il y a des tas de trucs qui ne servent à rien... Ou du moins qu'on oublie vite!

par **Babe** » 01 Avr 2008, 06:13

Rain' a écrit:Mais pour trouver la dimension de Co y a quand même plus simple que l'évaluer directement par la condition de normalisation, suffit de voir que cette intégrale est sans dimension

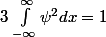
et donc que Co² à la dimension de l'inverse d'une longueur.

oui c'est comme cela que j'avais fais mais je n'etais pas sur

Oscillateur Harmonique Quantique

Oscillateur Harmonique Quantique

Qui est en ligne