Notation en PC

[Anonyme]

Bonjour
Sans se soucier du sens mathématiques des notations, je m'intéresse à leur usage et leur signification en physique:
- dx/dt: c'est la dérivée pr 1 fonction à 1 variable?
- le meme quotient avec "D ronde" désiqne la dérivée pr 1 fonction à +sieurs variables.
- Qu'en est-il pour delta minuscule?
Si l'on considère séparément chaque membre du quotient: dt par exple, son sens est-il le meme selon que c'est (D ronde)t ou (delta minuscule)t??
Merci d'avance

[phenomene]

Bonjour, il y a déjà deux fils à ce sujet : celui-ci sur la distinction entre dérivée d'une fonction d'une variable et dérivée partielle d'une fonction de plusieurs variables, et celui-là sur la distinction entre différentielles exactes (désignées par ) et formes différentielles (que les physiciens notent avec lorsqu'elles ne sont pas exactes).

C'est vrai qu'on parle de mathématiques dans ces fils, et que c'est compliqué, mais on ne peut pas expliquer le sens de ces notations mathématiques sans cela !

En résumé :
On note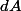 une différentielle exacte, la différentielle de la fonction . Pour un physicien, cela représente un "accroissement infiniment petit" de la fonction (ne me demandez pas ce que signifie "infiniment petit").
Les physiciens notent une forme différentielle. C'est une notation très dangereuse puisque la fonction n'existe pas. Pour eux, il s'agit d'une "quantité infiniment petite" mais qui n'est pas l'"accroissement infiniment petit" d'une vraie fonction.
Quant à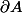 , ça ne veut rien dire, la notation 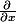est un "atome" (enfin, à la Epicure), c'est-à-dire qu'elle est insécable, numérateur et dénominateur n'ont aucun sens pris isolément. L'origine de cette notation est une simple analogie avec la notation utilisée pour les fonctions d'une variable dont on peut noter la dérivée avec un vrai quotient de différentielles (noté ) .

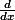Impossible d'en dire plus sans faire des maths... En espérant avoir été utlie.

[phenomene]

Ah, une explication "à la physicienne" pour expliquer la notation pour désigner la dérivée de la fonction .
Un physicien considère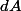 comme une variation infiniment petite de la fonction , et 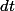comme un intervalle de temps infiniment petit. La dérivée de par rapport au temps représente la variation de pendant un intervalle infiniment petit, d'où la notation.

Bon, je vais me laver les mains. :soupir2: