bonsoir tt le monde...
avis au peuple: qqn saurait-il m'expliquer cmt déterminer des équations horaires ds les mvts plans????please.:dingue:
Mvts plans ==>équations horaires
4 messages
- Page 1 sur 1
par Julien S. » 06 Juin 2006, 20:24
C'est comme en une dimension:
r(t)=r0+v0*t+(1/2)*a*t^2
v(t)=v0+a*t
où r0 et v0 sont respectivement position et vitesses initiales et a l'accélération.
Sauf qu'il te faut remplacer r(t), v(t), r0, v0, et a par des vecteurs à deux composantes (si tu te restreint à un plan qui est donc bidimentionel).
J'espère t'avoir éclairé un peu!
r(t)=r0+v0*t+(1/2)*a*t^2
v(t)=v0+a*t
où r0 et v0 sont respectivement position et vitesses initiales et a l'accélération.
Sauf qu'il te faut remplacer r(t), v(t), r0, v0, et a par des vecteurs à deux composantes (si tu te restreint à un plan qui est donc bidimentionel).
J'espère t'avoir éclairé un peu!
par allomomo » 11 Juin 2006, 13:51
Salut,
Pour une chute libre :
<= Très important !
 \\v_y=-gt+C_2=-gt+v_0sin(\alpha)\\v_z=0})
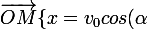t+C_3 \\y=-\frac{1}{2} gt^2+v_0sin(\alpha)t+C_4\\z=0})
On remplace dans y :
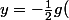^2+)
On travaille dans le plan :)
(car z=0)
Par exemple on nous demande de déduire l'équation de la trajectoire :
On a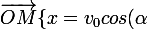t \\y=-\frac{1}{2} gt^2+v_0sin(\alpha)t\\z=0})
On va éliminer le paramètre temps.
alors :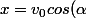t \Longleftrightarrow t=\frac{x}{v_0cos(\alpha)})
On remplace dans y :
})^2+v_0sin( \alpha )(\frac{x}{v_0 cos(\alpha )}))
Donc }+xtan(\alpha)})
Par exemple on nous demande de déterminer
(sommet de la trajectoire)
Au sommet de la trajectoire
}+tan(\alpha))
 v_{0}^{2}cos^2(\alpha) }{g}=\frac{sin(\alpha)}{cos(\alpha)}\frac{v_{0}^{2}cos^2(\alpha)}{g}=\frac{v_{0}^{2}cos(\alpha) sin(\alpha)}{g})
On remplace dans l'équation de la trajectoire :
 sin(\alpha)}{g})^2}{2v_{0}^{2}cos^2( \alpha ) }+(\frac{v_{0}^{2}cos(\alpha) sin(\alpha)}{g})tan(\alpha) =-\frac{v_{0}^{2}sin^2(\alpha)}{2g}+\frac{2v_{0}^{2}sin^2(\alpha)}{2g}=\frac{v_{0}^{2}sin^2(\alpha)}{2g})
Donc :}{2g}})
Pour une chute libre :
On remplace dans y :
On travaille dans le plan :
Par exemple on nous demande de déduire l'équation de la trajectoire :
On a
On va éliminer le paramètre temps.
alors :
On remplace dans y :
Donc
Par exemple on nous demande de déterminer
Au sommet de la trajectoire
On remplace dans l'équation de la trajectoire :
Donc :
par allomomo » 11 Juin 2006, 14:44
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :