Mouvement circulaire uniforme

[Anonyme]

Bonjour,

On se place dans le repere de Frenet.
Pourquoi un mouvement circulaire uniforme a Vx=cte , ax=0 et ay=cte ?
Et comment demontrer la reciproque si un mouvement a .... alors il est circulaire uniforme ?

Merci

[Ben314]

Bonjour,
Pour le sens direct, il suffit d'écrire dans un repère centré au centre du cercle et où est une base orthonormé du plan dans lequel le mobile se déplace.
Tu dérive une fois puis deux fois et.... tu constate que ça marche.

Pour la réciproque, tout d'abord deux remarques :
1) Il faut être en dimension 2 pour que la réciproque soit vrai ou bien rajouter dans les hypothèses que la torsion est nulle pour que le mouvement soit planaire.
2) L'hypothése V=cst n'est pas utile car ax=0 signifie que M'(t) est perpendiculaire à M''(t) c'est à dire que =0 (produit scalaire) or, 2 est la dérivée de =||M'(t)||² donc =0 implique que ||M'(t)||=cst.

Ton hypothèse (en dim 2) ce traduit alors par avec k une constante non nulle, c'est à dire d'où qui peut s'écrire (en changant l'origine du repère) .
On en déduit que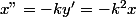 équation différentielle bien connue qui donne les solutions....