Qu. 1 :
Je vois pas d'où tu sors la relation finale, tu la sors de ton chapeau magique ? Aussi,
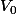
tu considères que c'est la vitesse initiale de quoi ? Sachant que ça n'a pas trop de sens de prendre en compte la vitesse initiale parce qu'on considère un problème stationnaire (le réservoir en amont est un pressostat puisque son volume varie peu au cours du temps, donc il impose a priori un débit constant durant l'échelle de temps de l'étude).
Non, la relation de Torricelli

vient naturellement de l'équation de Bernoulli que tu ne dois sans doute pas connaître puisque tu n'as pas commencé le cours.
COURS) Point cours (de mon cru) rapide alors :
Les équations de Navier-Stokes décrivent le comportement d'un fluide Newtonien incompressible :

(conservation de la masse)

, qu'on écrit aussi (en cartésiennes) :

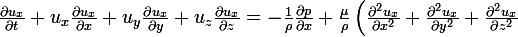 + f_x)
(conservation de la qté de mvmt selon x)
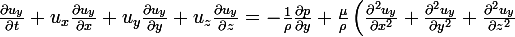 + f_y)
(conservation de la qté de mvmt selon y)
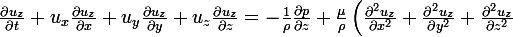 + f_z)
(conservation de la qté de mvmt selon z)
C'est un peu HS, mais si tu veux savoir comment on obtient ces équations, d'illustres Messieurs se sont évertués à écrire un PFD dans le cadre de la mécanique des milieux continus. Ils ont introduit le tenseur des contraintes dans l'équation de Newton que tu connais, et ont trouvé des modèles semi-empiriques visant à décrire le comportement de différents types de matériaux. En outre, les fluides visqueux ont le comportement décrit ci-dessus.
A partir de ces équations très générales, on va trouver l'équation de Bernoulli. Considérons que la seule force extérieure s'appliquant sur le fluide est la pesanteur (force conservative donc dérivant d'un potentiel), que l'écoulement est stationnaire (dérivée temporelle nulle) et parfait : Nous négligeons les contraintes visqueuses et considérons que l'écoulement est adiabatique. Nous trouvons l'équation d'Euler (utilisée pour les écoulements à nombre de Reynolds élevés, écoulements supersoniques, etc.) :

Intégrons désormais cette équation le long d'une ligne de courant

(une ligne de courant est une courbe à laquelle le champ de vitesse eulérien du fluide est tangent pour un temps t fixé) :
\right)\cdot \underscore{\mathrm{d}l} = \int_{\gamma}-\left(\frac{1}{\rho}\nabla p + \nabla(gz)\right)\cdot\underscore{\mathrm{d}l})
Nous avons alors :
\right)\cdot \underscore{\mathrm{d}l} = 0)
car l'écoulement est stationnaire.
Donc on trouve que le long d'une ligne de courant, la vitesse du fluide satisfait à l'équation suivante :

C'est l'équation de Bernoulli, qui établit une loi de conservation entre énergie cinétique du fluide (terme en u²), énergie potentielle (terme traduisant le dénivelé) et forçage (la pression). A partir de là, nous comprenons que le fluide est mis en mouvement (comportement mis en exergue par l'énergie cinétique du fluide) grâce à une énergie latente dû au poids du fluide et à des différences de pression (cf. différences de potentiels en électrostatique). Nous retrouvons de cette manière l'interprétation intuitive et tant utilisée en électronique : Un différentiel de potentiel engendre un flux.
A partir de là, il est tout à fait trivial d'aboutir au résultat de Torricelli ! Dans le cas qui nous incombe de traiter, nous isolons une ligne de courant (par définition stationnaire donc définie dans l'espace) dans le fluide, partant de la surface libre du fluide contenu dans le réservoir et aboutissant à la sortie de la turbine.
Puisque la vitesse du fluide au niveau de la surface libre est nulle (le réservoir est un pressostat), que la pression y est atmosphérique (idem en sortie), nous avons l'identité suivante :

2) Largeur superficielle ? Profondeur moyenne ? Hé il faut que tu fasses attention à ce que tu lis sur le net ! Là tu me fais le cas d'un écoulement à surface libre en utilisant aveuglément (et bêtement) des grandeurs que tu ne comprends pas.
Ici, il suffit en effet de multiplier vitesse en sortie et section de sortie pour trouver le débit en sortie. Puisque nous faisons l'hypothèse d'un fluide incompressible (raisonnable, car nous travaillons avec de l'eau), alors ce débit se conserve sur tout tube de courant et donc dans tout le tuyau. Sauf que la section de sortie est simplement un disque de rayon 4 cm... faut pas chercher midi à quatorze heures.
3) Dans la section E, que vaut la vitesse du fluide ?
4) On verra après, j'ai fait un message un peu long, essaie de tout lire d'abord et réponds à mes questions.