Bonjour, je sèche depuis plusieurs jours sur un problème de mécanique dont l'objet est la transformation d'une sphère en feuille plane. La sphère initiale est de rayon
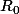
, on s'y repère en coordonnées sphériques
)
. On se repère sur la feuille plane finale en cartésiennes
)
. La transformation utilisée est la suivante, f étant une fonction donnée :
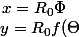)
J'ai calculé le gradient de la transformation :
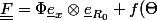\underline{e}_y \otimes \underline{e}_{R_0} + \frac{df}{d\Theta} \underline{e}_y \otimes \underline{e}_{\Theta} + \frac{1}{\sin \Theta}\underline{e}_x \otimes \underline{e}_\Phi)
Et ensuite on me demande d'étudier la dilatation surfacique... J'ai la formule
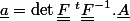
qui permet de calculer cette dilatation, sauf que je n'arrive pas à calculer
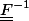
.
J'ai essayé en posant a priori
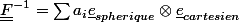
et en résolvant le système
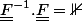
, mais je tombe sur des incohérences. Et quand j'essaye de calculer le gradient de la transformation inverse, je tombe également sur des trucs bizarres...
Merci d'avance.