Forces, mécanique de Newton
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 15 Fév 2008, 16:49
par farator » 15 Fév 2008, 16:49
Salut,
j'ai un exercice à faire sur les forces.
le voici Seulement je bloque sur la 4eme question de la partie une.
Je sais que
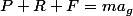
Mais je ne sais pas comment transformer R ...
Merci d'avance

 par Dominique Lefebvre » 15 Fév 2008, 18:31
par Dominique Lefebvre » 15 Fév 2008, 18:31
farator a écrit:Salut,
j'ai un exercice à faire sur les forces.
[url="http://labolycee.org/2005-Pondichery-Sujet-Exo2-MVtPalet-5-5pts.doc"]le voici[/url]
Seulement je bloque sur la 4eme question de la partie une.
Je sais que

Mais je ne sais pas comment transformer R ...
Merci d'avance

Bonsoir,
Je présume que ce que tu appelles
R est la réaction du support? Si oui, tu dois avoir noté qu'on néglige les frottements dans cette partie du problème. Dès lors, que sais-tu de la réaction du support en l'absence de frottement?
Au fait, une remarque: le PFD (ou deuxième loi de Newton) donne une égalité vectorielle. En employant la convention standard (met des flèches si tu veux...), il faut écrire
P +
R +
F = m
a
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 15 Fév 2008, 18:44
par farator » 15 Fév 2008, 18:44
Oui, j'ai appelé R la valeur de la force de réaction du support. Si je me rappelle des cours de l'année dernière, la réaction du support est perpendiculaire au support en l'absence de frottements ?
Ok pour le P+F+R=ma ...
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 15 Fév 2008, 18:56
par farator » 15 Fév 2008, 18:56
Je me trompe, ou
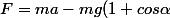)
??
 par Dominique Lefebvre » 15 Fév 2008, 19:00
par Dominique Lefebvre » 15 Fév 2008, 19:00
farator a écrit:Oui, j'ai appelé R la valeur de la force de réaction du support. Si je me rappelle des cours de l'année dernière, la réaction du support est perpendiculaire au support en l'absence de frottements ?
Ok pour le P+F+R=ma ...
Oui,
R est orthogonal à l'axe xx'
 par Dominique Lefebvre » 15 Fév 2008, 19:11
par Dominique Lefebvre » 15 Fév 2008, 19:11
farator a écrit:Je me trompe, ou

??
Je ne suis pas sûr de bien te suivre...
Récapitulons: le palet est en mouvement accéléré ascendant sur l'axe xx'.
Il n'y a pas de frottement donc la réaction du support R est équilibrée par le projeté du poids
p sur l'axe yy' orthogonal à xx' . Donc R = -mg*cos(alpha). C'est équilibré, on ne s'en occupe plus.
Sur l'axe xx' on a
F +
p*sin(alpha) = m
a. Je n'ai pas l'impression que la projection de cette égalité vectorielle sur ton référentiel donne le résultat que tu trouves....
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 15 Fév 2008, 19:28
par farator » 15 Fév 2008, 19:28
Sur l'axe xx' on a F + p*sin(alpha) = ma. Je n'ai pas l'impression que la projection de cette égalité vectorielle sur ton référentiel donne le résultat que tu trouves....
Ca je n'ai pas compris ...

ça d'accord, j'ai compris (j'avais oublié le -)
Donc :
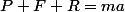
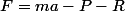

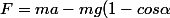)
Non ?
 par Dominique Lefebvre » 15 Fév 2008, 19:41
par Dominique Lefebvre » 15 Fév 2008, 19:41
farator a écrit:Ca je n'ai pas compris ...

ça d'accord, j'ai compris (j'avais oublié le -)
Donc :




Non ?
Ta projection de
p sur ton référentiel est fausse :
p a deux composantes : p*sin(alpha) sur l'axe xx' et p*cos(alpha) sur l'axe yy', cette dernière composante équilibrant R.
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 15 Fév 2008, 19:49
par farator » 15 Fév 2008, 19:49
Oui j'ai compris, c'est en fait les coordonnées de P dans le référentiel,
xp = -p*sin(alpha) et yp = -p*cos(alpha) ..
Mais je ne vois pas comment trouver la valeur R
ps: désolé si c'est encore un problème banal de "plan incliné" ^^
référence à la discussion "et la physique?"
 par Dominique Lefebvre » 15 Fév 2008, 19:56
par Dominique Lefebvre » 15 Fév 2008, 19:56
farator a écrit:Oui j'ai compris, c'est en fait les coordonnées de P dans le référentiel,
xp = -p*sin(alpha) et yp = -p*cos(alpha) ..
Mais je ne vois pas comment trouver la valeur R
ps: désolé si c'est encore un problème banal de "plan incliné" ^^
référence à la discussion "et la physique?"
As-tu fait un joli schéma avec un référentiel xGy centré sur le centre d'inertie du palet ?
Si oui, tu places le poids, à la verticale orienté vers le bas.
R est sur l'axe Gy orientée vers le haut. Le module de
R est à mg*cos(alpha).
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 15 Fév 2008, 20:39
par farator » 15 Fév 2008, 20:39
Bon,
on a la valeur P=mg
on a le module de R et donc la valeur R= mg*cos(alpha)
Je vois pas le problème, il suffit de remplacer P et R dans l'égalité P+F+R=ma et on peut facilement isoler F ...
 par Dominique Lefebvre » 15 Fév 2008, 22:17
par Dominique Lefebvre » 15 Fév 2008, 22:17
farator a écrit:Bon,
on a la valeur P=mg
on a le module de R et donc la valeur R= mg*cos(alpha)
Je vois pas le problème, il suffit de remplacer P et R dans l'égalité P+F+R=ma et on peut facilement isoler F ...
Fais attention:l'égalité que tu écris est une égalité vectorielle! Pour passer aux modules, il faut projeter sur les différents axes du référentiel. Et
P a deux projections (c'est le seul vecteur dans ce cas ici..) : une composante sur Gx et une sur Gy, resp. mg*sin(alpha) et mg*cos(alpha). Tu dois en tenir compte lorsque tu veux poser ton équation avec les modules des forces, sans oublier d'affecter les bon signes!
Si tu procèdes avec rigueur, il n'y a aucun problème....
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 16 Fév 2008, 11:54
par farator » 16 Fév 2008, 11:54
Bon, cette fois Dominique je suis quasiment sûr d'avoir trouvé ! :we:
Je me compliquais la vie.
Alors, on part de P+R+F=ma
Projection sur l'axe xx' : -sin(\alpha)*mg+0+F=ma (sur xx')
Le palet n'a aucun mouvement sur l'axe yy'
Donc -sin(\alpha)*mg+0+F=ma
F=ma+mg*sin(alpha)=m(a+g*sin(alpha))
Voilà .. ?
(et je n'ai pas ajouté les petits G après les a, mais je ne les oublie pas ..)
 par Dominique Lefebvre » 16 Fév 2008, 13:13
par Dominique Lefebvre » 16 Fév 2008, 13:13
farator a écrit:Bon, cette fois Dominique je suis quasiment sûr d'avoir trouvé ! :we:
Je me compliquais la vie.
Alors, on part de P+R+F=ma
Projection sur l'axe xx' : -sin(\alpha)*mg+0+F=ma (sur xx')
Le palet n'a aucun mouvement sur l'axe yy'
Donc -sin(\alpha)*mg+0+F=ma
F=ma+mg*sin(alpha)=m(a+g*sin(alpha))
Voilà .. ?
(et je n'ai pas ajouté les petits G après les a, mais je ne les oublie pas ..)
C'est déjà mieux!! En fait, si tu procèdes méthodiquement en traçant ton référentiel, en projetant convenablement tes vecteurs sur ce référentiel et en établissant les équations sans faire d'erreur de signe (signes qui dépendent de ton référentiel), alors un problème de méca est très simple.....
Bon, continue maintenant!
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 16 Fév 2008, 13:18
par farator » 16 Fév 2008, 13:18
C'est bon sinon, j'ai tout fait ...
Il suffit de remplacer par les valeurs pour la question suivante et le reste ne m'a pas posé de problèmes.
Voilà, merci beaucoup :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
??