Fonction de transfert

[MacErmite]

Bonjour,

Je bloque sur un problème qui me semblait pourtant simple à résoudre. Mais je suis coincé devant ceci :

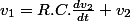
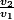
Je cherche a exprimer mais je tourne en rond :mur:

Pouvez-vous m'aider ?

Merci

[Skullkid]

Bonjour, s'il s'agit bien de calculer la fonction de transfert d'un circuit électronique comme les notations semblent l'indiquer, tous les calculs doivent se faire avec les amplitudes complexes (ou en Fourier, si tu connais le terme). Commence donc par traduire ton égalité avec les amplitudes complexes.

[Olympus]

Salut !

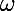
Dériver la fonction complexe associée à un signal de pulsation c'est multiplier par ... :we:

Je déplace vers la partie Physique

[MacErmite]

Bonjour, s'il s'agit bien de calculer la fonction de transfert d'un circuit électronique comme les notations semblent l'indiquer, tous les calculs doivent se faire avec les amplitudes complexes (ou en Fourier, si tu connais le terme). Commence donc par traduire ton égalité avec les amplitudes complexes.

Je n'ai pas assé de connaissance pour cela :marteau:

[Olympus]

Vous n'avez pas travaillé avec les grandeurs complexes en électricité ?

[MacErmite]

Vous n'avez pas travaillé avec les grandeurs complexes en électricité ?

je connais les formules d'Euler. Mais la forme complexe de l'équation en question, je ne vois pas comment procéder.
Peut-être dois-je utiliser les impédances : Zc=1/(Jcw), Zr=R. Mais il n'y a pas exponentielles ...

[Skullkid]

Tu as titré ton topic "fonction de transfert", donc tu dois bien avoir un cours qui porte sur les fonctions de transfert, et qui parle d'amplitudes complexes et/ou de transformées de Fourier.

[MacErmite]

je viens de lire une approche avec Laplace, ce qui donne :
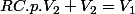
d'ou

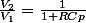
Je n'ai plus cas apprendre Laplace.

Etre autodidacte n'est pas de tout repos

[Black Jack]

je viens de lire une approche avec Laplace, ce qui donne :
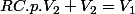
d'ou

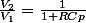
Je n'ai plus cas apprendre Laplace.

Etre autodidacte n'est pas de tout repos

Très souvent (mais pas toujours), la fonction de transfert est demandée pour un signal d'entrée sinusoïdal.
La fonction de transfert est alors exprimée en fonction de la pulsation w du signal d'entrée.

On a alors la correspondance immédiate entre l'''approche de Laplace" et la relation en fonction de w en remplaçant le "p" de Laplace par "jw"

On a alors (en sinusoïdal) : V2/V1 = 1/(1 + jwRC)

Il est alors immédiat de tracer la courbe de la fonction de transfert en fonction de w (avec w = 2.Pi.f)

|V2/V1| = 1/V(1 + w²R²C²) et arg(V2/V1) = -arctg(wRC)

:zen: