Filtres : problème de cours

par **pouik** » 14 Jan 2007, 13:17

Bonjour,
Je suis en train d'apprendre mons cours sur les Filtes (en MPSI) et je me rends compte que je ne sais pas du tout quand on a une fonction de transfert déterminer la pente de l'asymptote + le déphasage.

Si vous pouviez m'expliquer sur des exemples, ce serait formidable.

par **flaja** » 14 Jan 2007, 15:57

bonjour
voir : http://fr.wikipedia.org/wiki/Diagramme_de_Bode

par **pouik** » 14 Jan 2007, 16:14

désolé mais ils n'xepliquent pas grand-chose sur comment trouver le déphasage.. :
Par exemple, je propose la fonction de transfert :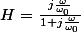

et donc dans mon livre il disent ensuite que :

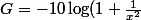et

Déjà là je ne vois pas du tout d'où sortent ces résulats !
Ensuite ils diesnt que : pour x -> 0, GdB -> 20 log x
et là une fois de plus je ne comprnds pas d'où ça sort !

Si vous pouvez m'expliquer ...

par **flaja** » 14 Jan 2007, 16:26

voir : http://fr.wikipedia.org/wiki/Filtre_passe-haut
avec x = omega / omega0

remarque : -10 lg(1/x²) = -10 lg(x^-2) = +20 lg(x)

par **pouik** » 14 Jan 2007, 16:31

je ne comprends pas la dernière égalité dans :

par **flaja** » 14 Jan 2007, 17:56

H = x / (1+x)
avec x = j omega/omega0
arg(H) = arg(x) - arg(1+x) = pi/2 - arctan(omega/omega0)

rappel : (a + j b) = sqrt(a²+b²) exp(j arctan(b/a))

par **pouik** » 14 Jan 2007, 18:14

d'accord mais pour apsser du membre de gauche à celui de droite :
-\arg(1+j\frac{\omega_c}{\omega})= \frac{\pi}{2} - \arctan(\frac{\omega}{\omega_c})

comment fait-il ?

PS : Désolé mais j'arrive pas à le compiler comme il faut : à la place de ce que j'ai mis, ca me met : f(x) = x²

par **flaja** » 16 Jan 2007, 22:56

bonsoir,
1)

Dans le plan complexe z=x + iy : x=1 et y =

d'où : tan(argument) = y/x
Et :

2) quand tu commences une formule par "moins", latex ne comprend pas
il faut mettre un espace avant tel que : \; par exemple
-x = 1 donne :

\; -x = 1 donne :

Filtres : problème de cours

Filtres : problème de cours

Qui est en ligne