Fermeture d'un bassin par une bille. ϴρ

[mimix]

Bonjour,

Une sphère de bois de masse volumique et de rayon R est complètement immergée dans un bassin d'eau, de masse volumique e de profondeur H de telle manière qu'elle bouche un trou circulaire de rayon r. J'ai essayé de représenter le plus fidèlement le schéma. On me demande de calculer la force que la sphère exerce sur le fond du bassin. Il y a pas mal de trucs que je ne comprends pas dans la correction:

La pression en un point de cote z dans l'eau est donnée par P(z) = Pa + eg(H-z). En fonction de l'angle des coordonnées sphériques, on obtient:

P(;)) = Pa + eg(H+R(cos;)0-cos;))), où 0 représente la valeur de au niveau de l'ouverture circulaire.

Comment fait-on pour obtenir cette expression?

De même, on me dit que dFz= (P(;)) - Pa)x(-cos;))dS)). Je ne comprends pas le terme en gras. Pa est la pression de l'air.

Merci.



Uploaded with ImageShack.us

[Mathusalem]

Salut.

Ils ont simplement exprimé z en fonction de R est de theta, ou theta est l'angle entre la verticale et le vecteur rayon. Si tu fais la projection, c'est bien le long de z.

[mimix]

Bonsoir :)

dFz= (P(;)) - Pa)x(-cos;))dS))

D'où vient (P(;)) - Pa)?

[mimix]

en faite c'est bon merci

[Mathusalem]

tu me diras si je pense juste, mais ça vient de la pression de la colonne d'air sous la roue qui le pousse résiste, d'où le -Pa

[mimix]

en faîte, c'est une boule, donc sa surface est fermée, et le vecteur dS orienté vers l'extérieur. Pour la pression exercée par l'air sous la boule, dS est orienté vers le bas, d'où le - Pa.dS.

J'ai une autre question, pourquoi est-ce que la profondeur est de (H-z)? pourquoi ce n'est pas H?

[Mathusalem]

Ce n'est pas la profondeur qui est (H-z).
C'est la pression en fonction de z.

z est pris vers le haut et a son commencement au niveau du trou. Donc pour z = 0, la pression de la colonne d'eau est de Pa + pg(H-z) = Pa + pgH

A une hauteur H au-dessus de l'embouchure, t'as plus que l'air => P(H) = Pa + Pg(H-H) = Pa

[mimix]

Oui, en faîte je m'étais embrouillée j'étais partie sur d'autres exos, et on veut en faite calculer la résultante des forces de pression qui s'exerce sur S, donc tous les points M appartenant à S de côte z!

J'ai une autre question, maintenant c'est le (-costheta) qui me gène.Je trouve bien P(theta) - Pa, mais pour dS (en vecteur) qd je le projette sur uz, je fais comment? J'ai dS en haut pour la partie supérieure, et dS en bas pour la partie inférieure...

[mimix]

J'ai une autre question,
si je découpe cette sphère en couronnes, celles-ci ont pour surface:

dS = 2piR²d(theta) non?

pourquoi a-t-on dS= 2piR²sin(theta)d(theta)

[Mathusalem]

J'ai une autre question,
si je découpe cette sphère en couronnes, celles-ci ont pour surface:

dS = 2piR²d(theta) non?

pourquoi a-t-on dS= 2piR²sin(theta)d(theta)

Si tu découpes cette sphère en couronnes,
Tu as pour un disque, le rayon R' relatif du disque est Rsin(theta) (projection sur l'horizontale de R).

Dès lors, l'aire de ton disque est .

Cependant le dS est un élément de surface de la sphère, pas d'un disque. Si tu appelles couronne la surface d'une bande circulaire sur la surface de la sphère, alors ton calcul est faux.
Selon toi, l'aire de la bande est identique que tu aies ou Imagine bien que si ton rayon R est vertical, ton expression n'a aucun sens, puisqu'alors la bande devrait être d'aire nulle.


Soit une sphère de rayon R.

Alors, tu essaies de dire ce que vaut "un petit rectangle" calqué sur la surface de la sphère. (Fais un dessin de ce que je raconte, ca deviendra clair)

Premièrement, tu considères un angle quelconque.

Pour cet angle , le rayon du cercle horizontal pour cette hauteur possède un rayon
Ainsi, te donne une section horizontale (une des base du rectangle).

En revanche, la "hauteur" du rectangle est simplement (tu balayes la sphère de haut en bas).
La multiplication des deux te donne une espèce de rectangle calqué sur la surface de la sphère.
Ainsi, .
En intégrant sur tout un tour horizontal (couronne), tu intègre sur et puisque rien n'en dépend, il vient sans autres

EDIT: C'est noël, voilà l'image
http://img163.imageshack.us/img163/9288/slide1cq.jpg

[mimix]

Je regarde votre réponse tout de suite, mais sauriez-vous pourquoi on a (-costheta)? d'où vient le moins svp?

merci pour votre aide :)

[Mathusalem]

Je regarde votre réponse tout de suite, mais sauriez-vous pourquoi on a (-costheta)? d'où vient le moins svp?

merci pour votre aide

Parce que la pression est linéaire dans le sens où elle ne dépend que de z. Ainsi, une colonne d'eau (pression qui varie que selon z) applique une force égale à . Or tu vois bien que la hauteur du cylindre, colonne, est H, et la surface est la surface EFFECTIVE. C'est à dire que tu ne regardes pas la surface sur la calotte sphérique, mais ce qu'elle vaut si tu la regardes frontalement.. 'fin sa valeur efficace quoi. Pour ça, tu peux projeter chaque élément de surface sur l'horizontale. Si tu regardes bien, tu retrouves entre la normale à la surface sphérique et un morceau tangent à cette surface (ds) l'angle theta... Pour projeter cette surface sur l'horizontale et ainsi obtenir sa valeur effective présentée contre la colonne d'eau, tu dois faire cos(theta).

Tu te retrouves avec Si tu intègres ça selon theta, tu obtiens bien , l'aire d'une section horizontale (disque) de la sphère, comme je t'ai expliqué plus haut.

Pour le signe moins
La pression est une grandeur scalaire. dFz en revanche est vectorielle. Le seul terme qui est vectoriel dans ta formule, c'est
Or par définition ce vecteur pointe vers l'extérieur de la surface..Donc en projetant la surface sur l'horizontale, il te vient un vecteur qui pointe vers le haut. Or, ta force va contre le bas -> signe moins.

[mimix]

Oui mais la pression exercée par l'air pointe vers le haut, avec un dS pointé vers le bas. En projetant sur l'axe horizontale, on garde le signe moins.
Pour celle exercée par l'eau, elle pointe vers le bas avec un dS orienté vers le haut, donc un moins qui se "transforme" en plus par projection sur l'horizontale.

d'où le P(theta) - Pa.

Ce qui me gène, c'est le (-costheta).dS donc la projection de dS sur l'horizontale.
dS peut être orienté vers le haut, dans les z positifs, dans ce cas on a (costheta)dS mais dans le cas où on est en dessous de la bille, vers l'air, dS est orienté vers les z négatifs, et dans ce cas, on a (-costheta)dS.

J'ai forcément une erreur dans mon raisonnement, et je ne comprends pas ce signe moins qui paraît convenir aux 2 pressions.

Peut-être que, comme les forces qui s'exercent sur la surface de la bille sont exercées par des fluides qui lui "sont extérieurs", on a le signe moins..

J'ai été habituée à avoir dF = PdS , dF étant la force exercée par le fluide à l'intérieur de la boule, sur sa surface. Si les fluides sont à l'extérieurs, ça revient à avoir le cas inverse non? et donc le moins?

[Mathusalem]

Non non non tu t'embrouilles.

Sépares les termes en 2:

= P(;))(-cos;)))) - Pa(-cos(;))))

P(;)) c'est la pression de l'eau sur la boule (+ l'atmosphère d'en dessus). Dans cette zone, dS est dirigée vers le haut, or l'eau appuye sur la boule, donc la force va vers le bas. Ici, c'est cohérent, ça donne

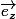
Donc une force qui pointe vers le bas, puisque pointe vers le haut

Pa c'est la pression de l'air par en-dessous de la boule
Ca donne


Donc une force qui pointe vers le haut.

Si Pa > P(;)), alors ta boule monte
si Pa < P(;)), alors la boule reste collée au fond.

Mais enfait, si tu regardes bien, dans P(;)) , t'as déjà un P(a).
Ce qui revient à dire qu'au final, la force exercée sur ta boule, c'est que la contribution de la colonne d'eau, vu que les atmosphères se virent de part et d'autre de la boule.

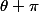
EDIT : Remarque bien en revanche que sur la partie inférieure, l'angle entre la surface tangente et le vecteur normal à la surface, c'est pas mais (car pour chaque bout tangent a la surface en haut, t'en as un symétrique sur la partie inférieure, i.e degrés plus loin), ce qui arrange tes signes et qui les explique dans mon calcul.

Mais ceci est une manière compliquée de réfléchir. Tu peux juste te dire " J'ai une surface qui vaut cos(theta)dS " (dS scalaire). Y a une pression qui va vers le bas (négative) , et une pression qui va vers le haut (positive) . L'addition des deux me donne la pression resultante sur la surface efficace

Si est positif, ca monte
si est négatif, ca descend.
Et tu te fais pas chier.