Exercice
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
Bourguignon
- Messages: 9
- Enregistré le: 23 Déc 2012, 13:21
-
 par Bourguignon » 29 Déc 2012, 15:26
par Bourguignon » 29 Déc 2012, 15:26
Bonjour,
On considère l'équation de Schrödinger libre en une dimension , = - \frac{\hbar ^2}{2m}\frac{d^2}{dx^2}\psi (x)) pour
pour  . On souhaite interdire l'accès a
. On souhaite interdire l'accès a 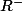 via une condition généralisée :
via une condition généralisée :
[CENTER]= \lambda\psi (0))
[/CENTER]
1) A quelle condition sur  la particule est elle contrainte à rester sur
la particule est elle contrainte à rester sur  ?
? Dans la correction il est dit que

doit être réél. Pas de soucis.
2)Résoudre l'équation de Schrödinger et discuter des cas limites 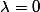 et
et  .
.Pour repondre à cette question, dans la correction, on commence par écrire la solution stationnaire sous la forme
= A (e^{ikx+2i\eta}+e^{-ikx}))
et j'ai l'impression que cette forme sort d'un chapeau magique... je ne vois pas pourquoi et de quel droit on utilise cette forme.
Cordialement,
Bourguignon.
-
herr_mulle
- Membre Naturel
- Messages: 97
- Enregistré le: 10 Nov 2012, 15:51
-
 par herr_mulle » 29 Déc 2012, 18:21
par herr_mulle » 29 Déc 2012, 18:21
Bourguignon a écrit:Bonjour,
On considère l'équation de Schrödinger libre en une dimension , = - \frac{\hbar ^2}{2m}\frac{d^2}{dx^2}\psi (x)) pour
pour  . On souhaite interdire l'accès a
. On souhaite interdire l'accès a 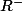 via une condition généralisée :
via une condition généralisée :
[CENTER]= \lambda\psi (0))
[/CENTER]
1) A quelle condition sur  la particule est elle contrainte à rester sur
la particule est elle contrainte à rester sur  ?
? Dans la correction il est dit que

doit être réél. Pas de soucis.
2)Résoudre l'équation de Schrödinger et discuter des cas limites 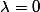 et
et  .
.Pour repondre à cette question, dans la correction, on commence par écrire la solution stationnaire sous la forme
= A (e^{ikx+2i\eta}+e^{-ikx}))
et j'ai l'impression que cette forme sort d'un chapeau magique... je ne vois pas pourquoi et de quel droit on utilise cette forme.
Cordialement,
Bourguignon.
Equation qui se met sous la forme : y"+omega^2.y=0
y-->Psy,
et omega^2=

+ \frac{\hbar ^2}{2m}\frac{d^2}{dx^2}\psi (x)=0)
+\frac{2.m.E}{\hbar ^2}\psi (x) =0)
dont les solutions sont y(x)=A.exp(i.omega.x)+B.exp(-i.omega.x)
(à condition que E>0, sinon les solutions sont en sinus et cos hyperbolique)
Discuter de lambda, c'est discuter en quelque sorte de E (niveau d'énergie), donc il faut trouver la relation entre lambda et omega et ainsi E.
si lambda=0, A=B
et on a : Psi=2.A.cos(omega.x)
si lambda-->infini,
A et B sont des imaginaires purs A=iK. K réel et très grand , on aura un déphasage de pi/2 car i=exp(i.pi/2)......voilà pour quelques pistes..........
Merci de confirmer que cela vous a aidé ou pas ....
-
Bourguignon
- Messages: 9
- Enregistré le: 23 Déc 2012, 13:21
-
 par Bourguignon » 30 Déc 2012, 18:20
par Bourguignon » 30 Déc 2012, 18:20
Re, tout d'abord merci pour ton aide.
Moi comme solution de cette équation j'aurais mis
=A.e^{ikx}+B.e^{-ikx})
sur
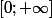
car c'est une onde propagative si

.
Ton omega correspond à mon k je pense...
Mais ce que je voulais savoir c'est pourquoi et comment ils peuvent utiliser la forme
= A (e^{ikx+2i\eta}+e^{-ikx}))
. C'est quoi ce

, d'où il sort ?
Voilà la correction intégrale du 2)Écrivons la solution stationnaire sous la forme
= A (e^{ikx+2i\eta}+e^{-ikx}))
. En imposant
 = \lambda \psi(0))
on obtient

. La solution est
 = \sqrt{2/\pi} cos(kx+\eta ))
, normalisée pour que
 \psi_{k'} (x))
=

(k-k'). La limite quand
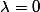
correspond à une condition de Neumann
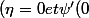 = 0 ))
et

à une condition de Dirichlet (

et
=0)
)
-
herr_mulle
- Membre Naturel
- Messages: 97
- Enregistré le: 10 Nov 2012, 15:51
-
 par herr_mulle » 30 Déc 2012, 19:33
par herr_mulle » 30 Déc 2012, 19:33
Mais est-ce que

est la dérivée de

par rapport à x ? Je ne connais pas le contexte de ce travail. Et c'est aussi cela qui peut être dur pour un contributeur.
-
Bourguignon
- Messages: 9
- Enregistré le: 23 Déc 2012, 13:21
-
 par Bourguignon » 30 Déc 2012, 19:37
par Bourguignon » 30 Déc 2012, 19:37
Oui je pense car psi est fonction de x. Il n'y a pas vraiment de contexte, j'ai vraiment mis l'exo tel qu'il apparaît sur mon livre
-
herr_mulle
- Membre Naturel
- Messages: 97
- Enregistré le: 10 Nov 2012, 15:51
-
 par herr_mulle » 30 Déc 2012, 19:39
par herr_mulle » 30 Déc 2012, 19:39
1) A quelle condition sur \lambda la particule est elle contrainte à rester sur R^+ ?
Dans la correction il est dit que \lambda doit être réél. Pas de soucis.
On a typiquement un oscillateur Harmonique, la solution stabe se trouve au fond de la parabole. Je pense que Lambda doit être positif pour que la particule va vers les x>0.
-
herr_mulle
- Membre Naturel
- Messages: 97
- Enregistré le: 10 Nov 2012, 15:51
-
 par herr_mulle » 30 Déc 2012, 19:42
par herr_mulle » 30 Déc 2012, 19:42
Bourguignon a écrit:Oui je pense car psi est fonction de x. Il n'y a pas vraiment de contexte, j'ai vraiment mis l'exo tel qu'il apparaît sur mon livre
Dire que Feynman a dit :
Je crois pouvoir dire à coup sur que personne ne comprend la mécanique quantique, et avec des énoncés comme cela, les étudiants ne sont pas près de comprendre.
-
herr_mulle
- Membre Naturel
- Messages: 97
- Enregistré le: 10 Nov 2012, 15:51
-
 par herr_mulle » 30 Déc 2012, 19:45
par herr_mulle » 30 Déc 2012, 19:45
Il faut que j'y réfléchisse à tête reposée, et à ventre plein. Bonsoir.
-
Bourguignon
- Messages: 9
- Enregistré le: 23 Déc 2012, 13:21
-
 par Bourguignon » 30 Déc 2012, 19:48
par Bourguignon » 30 Déc 2012, 19:48
herr_mulle a écrit:Dans la correction il est dit que \lambda doit être réél. Pas de soucis.
ça c'est moi qui l'ai écrit.
La correction pour la 1) dit que :
Le courant de propbabililé à l'origine ,
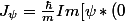 \psi ' (0)] = \frac{\hbar}{m} |\psi (0)|^2 Im(\lambda))
s'annule si
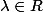
. Dans ce cas la particule reste sur

.
-
herr_mulle
- Membre Naturel
- Messages: 97
- Enregistré le: 10 Nov 2012, 15:51
-
 par herr_mulle » 30 Déc 2012, 20:57
par herr_mulle » 30 Déc 2012, 20:57
Bourguignon a écrit:Le courant de propbabililé à l'origine ,
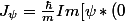 \psi ' (0)] = \frac{\hbar}{m} |\psi (0)|^2 Im(\lambda))
s'annule si
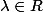
. Dans ce cas la particule reste sur

.
Désolé, je sèche encore plus avec la densité de probabilité.....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
