équation différentiel dans un circuit.

[Jjl]

Bonsoir,j'ai tenter de faire cet exercice


Toutefois comme vous pouvez le voir,j'ai eu du mal a exprimer Uc dans le (2).
J'ai aussi eu du mal à trouver la solution des équa diff ,ainsi qu'avec les autres questions aussi.
Mais voici toutefois ce que j'ai écrit:

[Pisigma]

Bonsoir,j'ai tenter de faire cet exercice


Toutefois comme vous pouvez le voir,j'ai eu du mal a exprimer Uc dans le (2).
J'ai aussi eu du mal à trouver la solution des équa diff ,ainsi qu'avec les autres questions aussi.
Mais voici toutefois ce que j'ai écrit:

Bonsoir,

Quelques remarques préliminaires:

Les grandeurs qui interviennent dans ton circuit sont des grandeurs variables en fonction du temps donc tu dois les écrire avec des lettres minuscules.

Tes tensions sont fléchées dans le mauvais sens car d'habitude on utilise la convention récepteur.

Il n'est pas nécessaire d'utiliser les mailles puisque E alimente directement deux branches en parallèle.

Tu trouveras ici http://www.noelshack.com/2015-50-1449694389-rlc-parallele-jjl001.jpg
une ébauche de solution, avec mes commentaires.

J'ai utilisé des variables plus explicites que V1,...

Je viens de me rendre compte que parfois j'ai utilisé i2 au lieu de ic. Je te laisserai corriger.

[Jjl]

Bonsoir,

Quelques remarques préliminaires:

Les grandeurs qui interviennent dans ton circuit sont des grandeurs variables en fonction du temps donc tu dois les écrire avec des lettres minuscules.

Tes tensions sont fléchées dans le mauvais sens car d'habitude on utilise la convention récepteur.

Il n'est pas nécessaire d'utiliser les mailles puisque E alimente directement deux branches en parallèle.

Tu trouveras ici http://www.noelshack.com/2015-50-1449694389-rlc-parallele-jjl001.jpg
une ébauche de solution, avec mes commentaires.

J'ai utilisé des variables plus explicites que V1,...

Je viens de me rendre compte que parfois j'ai utilisé i2 au lieu de ic. Je te laisserai corriger.

Pas de problème pour le i2,ahh enfin je vois comment on calcul ce Uc!
Merci beaucoup pour tes explications détaillé,cependant,t=0+ ça correspond à, quel temps?(mon prof nous parle jamais de 0+ ou 0-).
Bon là normalement je pourrais tracer les courbes qu'ils demandent.
Ensuite je tiendrais compte de tes conseils concernant les minuscules et les tensions.

[Pisigma]

Pas de problème pour le i2,ahh enfin je vois comment on calcul ce Uc!
Merci beaucoup pour tes explications détaillé,cependant,t=0+ ça correspond à, quel temps?(mon prof nous parle jamais de 0+ ou 0-).
Bon là normalement je pourrais tracer les courbes qu'ils demandent.
Ensuite je tiendrais compte de tes conseils concernant les minuscules et les tensions.

Cela signifie juste à la fermeture de l'interrupteur.

[Jjl]

Cela signifie juste à la fermeture de l'interrupteur.

Ah ok,gracias

[Pisigma]

Ah ok,gracias

De rien :lol3:

[Black Jack]

2)

E = R1.iL + L.diL/dt

iL = K.e^(-R1/L * t) + E/R1
iL(0) = 0 --> K = -E/R1

iL(t) = E/R1 * (1 - e^(-R1/L * t))
*****
E = R2.ic + Uc
avec ic = C.dUc/dt

R2.ic + dUc/dt = 0
R2.dic/dt + ic/C = 0

ic = K'.e^(-t/(RC))
ic(0) = E/R2 --> K' = E/R2

ic(t) = E/R2 * e^(-t/(R2.C))
*****
3)

a)

i(t) = ic(t) + iL(t)

i(t) = E/R2 * e^(-t/(R2.C)) + E/R1 * (1 - e^(-R1/L * t))


:zen:

[Pisigma]

2)

E = R1.iL + L.diL/dt

iL = K.e^(-R1/L * t) + E/R1
iL(0) = 0 --> K = -E/R1

iL(t) = E/R1 * (1 - e^(-R1/L * t))
*****
E = R2.ic + Uc
avec ic = C.dUc/dt

R2.ic + dUc/dt = 0
R2.dic/dt + ic/C = 0

ic = K'.e^(-t/(RC))
ic(0) = E/R2 --> K' = E/R2

ic(t) = E/R2 * e^(-t/(R2.C))
*****
3)

a)

i(t) = ic(t) + iL(t)

i(t) = E/R2 * e^(-t/(R2.C)) + E/R1 * (1 - e^(-R1/L * t))


:zen:

Salut Black Jack,

J'ai supposé que Jjl était capable de résoudre ces équations classiques :lol3:

[Black Jack]

Salut Black Jack,

J'ai supposé que Jjl était capable de résoudre ces équations classiques :lol3:

Salut Pisigma,

Cela fait belle lurette que je ne suppose plus rien du tout avec la qualité de l'enseignement actuel. :marteau:

:zen:

[Jjl]

Salut Pisigma,

Cela fait belle lurette que je ne suppose plus rien du tout avec la qualité de l'enseignement actuel. :marteau:

:zen:

Mdr,ça va Black jack?
C'est pas faux,l'enseignement actuelle n'est pas terrible,mais jvai pas mentir,certain étudiant sont partiellement responsable de leur problèmes aussi,c'est mon cas,jvai pas tout mettre sur le dos des profs,et puis même quand on a eu de mauvais profs,il faut travailler de son côté,chercher dans les livres,sur le net...
Ah oui,merci pour ton aide encore une fois,c'est sympa,merci a vous deux.

[jjl2]

Euh la question 3b) j'ai demandé un peu d'aide et voici ce qu'on m'as dit:
Pour la date correspondant au minimum de i(t), je ne vois pas plus simple qu'un calcul de dérivée : le minimum sera obtenu pour di(t)/dt = 0.
Pour trouver le moment où le courant est maximal ou minimal, dérivez i(t) et égalez à zéro.
Puis passez les deux exponentielles du même côté et les coefficients de l’autre.
Vous Aurez une équation du genre A = exp(b.t), dont il est facile de sortir ‘t’.
J'ai donc suivis ce conseil et écrit:

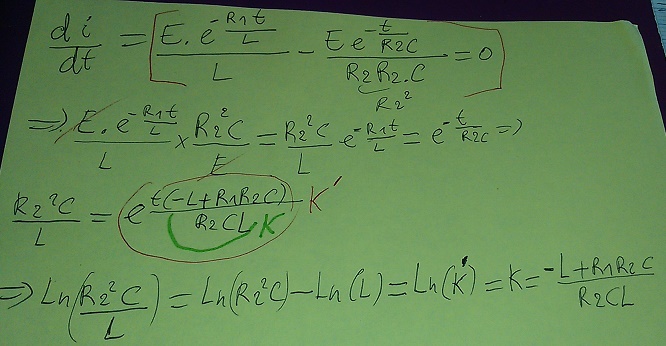
Mais est-ce bon?