Entropie

[Mathusalem]

Si tu veux connaître les vraies implications du deuxième principe, fais un peu des recheches sur internet. Tu verras qu'il y a des spécimens parmi la population américaine qui manifeste contre l'enseignement de la deuxième loi de la thermo. Une de mes connaissances sortant d'un lycée religieux américain s'est vu inculquer la notion que l'Entropie est le vilain, et que d'en parler était un péché.
Ceci montre deux choses : la bêtise n'est pas majorée, la deuxième loi va très loin.

The zeroth rule : There's a game you have to play
The first rule : You can't win
The second rule : You can't break even
The third rule : You can't quit

Humour assez populaire lié à la thermo.
A+

[Benjamin]

Dans toute transformation, . Et dans tous les cas, .

En gros, le 2e principe est en lui-meme presque inutile. Cependant, tu peux "combiner" la 2e et 1ere loi afin d'obtenir le principe de Carnot, qui est (tres) utile.

Bonjour,

Et la variation d'entropie interne, tu en fais quoi ? Ensuite, Q n'est pas une différentielle exacte. Il faut être précis, on utilise un delta dans ce cas.
Ainsi, pour toute transformation élémentaire, . est lié à l'irréversibilité des transformations internes au système. C'est l'entropie créée, qui est forcément positive ou nulle. Elle n'est nulle que dans le cas d'une transformation réversible. Sachant que dans la vraie vie, les transformations réversibles n'existent pas, ça serait gênant d'oublier cette variation d'entropie interne...

[Benjamin]

Petit cours sur le second principe :

Le second principe était nécessaire car le premier principe était insuffisant à expliquer ce qu'on on observait. Le premier principe est un principe de conservation de l'énergie :
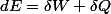. Dans le cas d'un système isolé, 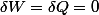donc dE=0 donc E=U+Em=cte : c'est ça la conservation de l'énergie.

Maintenant, considérons l'échange thermique entre deux solides dans une enceinte adiabatique. Q1 est la chaleur reçue par le solide 1 provenant du solide 2 et Q2 est la chaleur reçue par le solide 2 provenant du solide 1. Le premier principe montre que Q1+Q2=0 donc que Q1=-Q2. Mais en l'état, on voit qu'on peut choisir a priori Q10 ou Q1>0 et Q2T2, l'expérience montre que nécessairement, Q10 : les transferts d'énergie se font toujours du chaud vers le froid. Il faut donc un principe d'évolution qui permettent de rendre compte de ça : c'est le second principe.

On a alors défini une fonction d'état extensive : l'entropie (enfin, historiquement, ça a pas été clair au début, et l'entropie n'a été bien figée et définie que plus tard après sa première apparition !)
Pour toute évolution élémentaire, elle est la somme de 2 termes :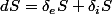 . Le terme est algébrique et est lié aux échanges entre le système et l'extérieur : c'est l'entropie d'échange. , c'est l'entropie créée, j'en ai parlé au-dessus.
Il se trouve que pour un système fermé (c'est-à-dire n'échangeant pas de la matière avec l'extérieur, mais juste de l'énergie),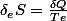 où Te est la température du système au niveau de sa frontière.

Pour que tu comprennes cette histoire de maximale : étudions le cas où le système est isolé :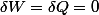 , E=cte (premier principe). Le second principe nous donne 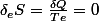donc 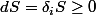. Quand le système évolue, il le fait irréversiblement car spontanément. L'inégalité est strict : dS>0 donc S augmente. En fait, l'augmentation d'entropie est une augmentation du désordre du système. On voit donc que le système évolue tant que l'entropie S peut augmenter. Quand S est maximale, le système n'évolue plus car il est en équilibre et on a dS=0.
Le second principe peut donc aussi s'énoncer comme ça : "L'évolution spontanée d'un système isolé se fait avec augmentation d'entropie. A l'équilibre, l'entropie est maximale."

[Mathusalem]

Merci pour ces quelques explications.

[barbu23]

Merci encore une fois pour ces precisions ! :happy3:

[Benjamin]

Avec plaisir, n'hésitez pas à demander des précisions.