tout compte fait, je vais reprendre tous les calculs à tête reposée ^^
Merci encore beaucoup pour ton aide Manoa :++:
Julie
Encore un peu de physics :p
31 messages
- Page 2 sur 2 - 1, 2
globule rouge a écrit:tout compte fait, je vais reprendre tous les calculs à tête reposée ^^
Merci encore beaucoup pour ton aide Manoa :++:
Julie
En multipliant par exp(-dt/2a) / exp(-dt/2a) le membre de droite de l'expression de Manoa, on voit du tanh(dt/2a) sortir.
En amont de cela, il y a une identité trigonométrique reliant (log(1+x) - log(1-x)) a arctanh(x). Je te laisse la chercher plus précisément
Mathusalem a écrit:En multipliant par exp(-dt/2a) / exp(-dt/2a) le membre de droite de l'expression de Manoa, on voit du tanh(dt/2a) sortir.
En amont de cela, il y a une identité trigonométrique reliant (log(1+x) - log(1-x)) a arctanh(x). Je te laisse la chercher plus précisément
Aaaahhh j'arrive finalement à trouver
Je vais regarder ce que tu m'as dit Mathusalem
Edit : je viens de me documenter un peu et cela me donne directement
Am I done with this ?
Salut,;)Petite precision. Pour chercher l'equivalence entre ton expression et l'arctangente hyperbolique dont je parlais avant, on part en cherchant l'inverse de la tangente hyperbolique. ;)
;)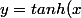 := \frac{sinh(x)}{cosh(x)})
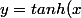 := \frac{e^{x} - e^{-x}}{e^x + e^{-x}})
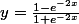 ;)Donc,
;)Donc,
 - 1 + e^{-2x} = 0) ;)
;)
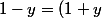e^{-2x})
 - ln(1-y)) = x)
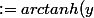 = x) ;);)
;);)
Maintenant a toi de porter ton expression sous cette forme afin de faire sortir l'arctangente hyerbolique.
Qu'est-ce que tu veux dire par logiciel pour tester ?
Maintenant a toi de porter ton expression sous cette forme afin de faire sortir l'arctangente hyerbolique.
Qu'est-ce que tu veux dire par logiciel pour tester ?
Mathusalem a écrit:Salut,;)Petite precision. Pour chercher l'equivalence entre ton expression et l'arctangente hyperbolique dont je parlais avant, on part en cherchant l'inverse de la tangente hyperbolique.;)
;)Donc,
;)
;);)
Maintenant a toi de porter ton expression sous cette forme afin de faire sortir l'arctangente hyerbolique.
Qu'est-ce que tu veux dire par logiciel pour tester ?
J'ai bien compris la technique qui consiste à faire ressortir l'argument tangente hyperbolique ^^ Mais ne faut-il pas juste trouver v(t) ? Je ne saisis pas la nécessité de faire les calculs que tu me propose.
Mais bon, je vais quand même m'y atteler pour voir
Bien, j'ai
[CENTER]
d'où [CENTER]
Et par suite : [CENTER]
Nous obtenons donc : [CENTER]
Ce qui implique : [CENTER]
Et finalement :
Mais je ne comprends pas à quoi cela pourrait me servir ^^
Ah oui, en ce qui concerne le logiciel de calcul formel, c'était pour vérifier la forme qu'aurait v(t), en testant divers paramètres !
Mais je pense qu'il n'est pas possible d'en trouver un fiable sur le net :triste:
Julie
globule rouge a écrit:J'ai bien compris la technique qui consiste à faire ressortir l'argument tangente hyperbolique ^^ Mais ne faut-il pas juste trouver v(t) ? Je ne saisis pas la nécessité de faire les calculs que tu me propose.
Mais bon, je vais quand même m'y atteler pour voir
Bien, j'aiqui autrement me donne :
[CENTER][/CENTER]
d'où [CENTER][/CENTER]
Et par suite : [CENTER][/CENTER]
Nous obtenons donc : [CENTER][/CENTER]
Ce qui implique : [CENTER][/CENTER]
Et finalement :
Mais je ne comprends pas à quoi cela pourrait me servir ^^
Ah oui, en ce qui concerne le logiciel de calcul formel, c'était pour vérifier la forme qu'aurait v(t), en testant divers paramètres !
Mais je pense qu'il n'est pas possible d'en trouver un fiable sur le net :triste:
Julie
L'utilité, c'est qu'une fois que t'as intégré la forme et que tu tombes sur du ln(1+y) - ln(1-y), tu t'embêtes pas à faire sortir le v(t) avec beaucoup d'opérations. Tu reconnais l'identité, et tu te retrouves avec de l'arctanh, que tu inverses easy pour te retrouver avec du tanh (forme finale de v(t)).
En fait, après l'intégrales, tu te trouves à ton avant-dernière ligne. L'identité te permet de passer à la dernière ligne, et avec ça, t'as le résultat de la première ligne qui tombe directement (t'as fait à l'envers ce que je voulais te faire faire)
Cherche des logiciels de graphe (si tu as un mac, de base il y a un software qui s'appelle Grapher qui est bien) sur internet.
A+ Math
manoa a écrit:@Mathusalem
Sympa le passage par tanh
@antonyme : c'est une version pro que tu as là ? :bad:
Oui, mais j'ai pas payer 300 euros t'inquiète pas... :lol3: Je n'en dirais pas plus, restons dans la légalité (non non, c'pas moi monsieur l'agent, j'vous jure j'est pas téléchargé illégalement :euh: )
antonyme a écrit:Oui, mais j'ai pas payer 300 euros t'inquiète pas... :lol3: Je n'en dirais pas plus, restons dans la légalité (non non, c'pas moi monsieur l'agent, j'vous jure j'est pas téléchargé illégalement :euh: )
S'il-te-plait !!! Je veux le même !!
Sinon, un grand merci à tous de m'avoir aidé dans la résolution de cette équation ^^
Vos conseils m'ont été précieux
A bientôt pour de nouvelles aventures !!
Julie
Ps : si j'ai d'autres questions je les posterai ici
31 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :


