Bonjour,
Je suis actuellement en train de plancher sur mon cours d'electrostatique et je dois dire que je suis bloqué avec le théoreme de Gauss. Tout d'abord je ne comprend pas la formule du débit :
D=;)V ;) .(dS) ;)
J'ai comme explication, dans une canalisation ou la vitesse n'est pas uniforme, on calcul le débit a travers des éléments de surface dS pour considérer la vitesse comme constante. Pour avoir le débit total il nous reste qu'a faire la somme.
La ou je bloque c'est au niveau de la formule. Parce que pour chaque dS la vitesse du fluide est différente. or dans l'intégral on en tient pas compte. V est considérer comme une constante. Je suis d'accord qu'elle soit constante pour chacun des dS et qu'elle valent 2m/s pour un certain dS puis 3m/s pour un autre dS mais ce n'est en aucun cas une constante dans l'intégrale .
Pouvez vous m'éclaircir ?
Merci D'avance
Débit ( en général)
5 messages
- Page 1 sur 1
Bonjour, la vitesse n'est pas considérée comme constante dans l'intégrale. Ce que ton texte explique c'est que l'idée de la formule, comme tu l'as dit, est de couper la surface en un très grand nombre de surfaces élémentaires, sur chacune desquelles on peut considérer la vitesse comme constante, et que le débit est défini comme la somme des produits vitesse*surface pour chacune des surfaces élémentaires. Ce qui te gêne c'est peut-être que la dépendance de v par rapport aux coordonnées n'apparaît pas explicitement dans la formule, mais en physique on n'écrit les dépendances que quand on considère qu'on en a vraiment besoin.
Par exemple pour une section circulaire de rayon R avec le champ de vitesses en polaires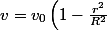) dirigé perpendiculairement à la section, le débit est
dirigé perpendiculairement à la section, le débit est 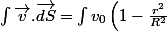rdrd\theta = \frac{\pi}{2}R^2 v_0) .
.
Par exemple pour une section circulaire de rayon R avec le champ de vitesses en polaires
Super !!! Merci beaucoup pour votre explication je ne suis finalement pas débile :ptdr: . Je me disais bien qu'il y a comme vous dite une relation pour v . Enfait la grande différence avec le théoreme de Gauss , c'est que le champ electrique dernier est considére comme constant dans l'integrale non ?
Skullkid a écrit:Bonjour, la vitesse n'est pas considérée comme constante dans l'intégrale. Ce que ton texte explique c'est que l'idée de la formule, comme tu l'as dit, est de couper la surface en un très grand nombre de surfaces élémentaires, sur chacune desquelles on peut considérer la vitesse comme constante, et que le débit est défini comme la somme des produits vitesse*surface pour chacune des surfaces élémentaires. Ce qui te gêne c'est peut-être que la dépendance de v par rapport aux coordonnées n'apparaît pas explicitement dans la formule, mais en physique on n'écrit les dépendances que quand on considère qu'on en a vraiment besoin.
Par exemple pour une section circulaire de rayon R avec le champ de vitesses en polairesdirigé perpendiculairement à la section, le débit est
.
Dans le théorème de Gauss le champ électrique n'est pas constant non plus. Le théorème dit que l'intégrale de la divergence du champ sur un volume est égale au flux du champ à travers la surface qui délimite ce volume (c'est d'ailleurs un théorème général d'analyse vectorielle).
Après, c'est toujours plus facile de calculer le flux du champ à travers une surface sur laquelle ledit champ est constant, c'est pour ça qu'on choisit de telles surfaces quand on peut. Par exemple pour une distribution de charges uniforme et sphérique, on va utiliser le théorème sur les sphères concentriques avec la distribution de charges. Mais il est aussi valable pour des surfaces plus exotiques.
Après, c'est toujours plus facile de calculer le flux du champ à travers une surface sur laquelle ledit champ est constant, c'est pour ça qu'on choisit de telles surfaces quand on peut. Par exemple pour une distribution de charges uniforme et sphérique, on va utiliser le théorème sur les sphères concentriques avec la distribution de charges. Mais il est aussi valable pour des surfaces plus exotiques.
Skullkid a écrit:Dans le théorème de Gauss le champ électrique n'est pas constant non plus. Le théorème dit que l'intégrale de la divergence du champ sur un volume est égale au flux du champ à travers la surface qui délimite ce volume (c'est d'ailleurs un théorème général d'analyse vectorielle).
Après, c'est toujours plus facile de calculer le flux du champ à travers une surface sur laquelle ledit champ est constant, c'est pour ça qu'on choisit de telles surfaces quand on peut. Par exemple pour une distribution de charges uniforme et sphérique, on va utiliser le théorème sur les sphères concentriques avec la distribution de charges. Mais il est aussi valable pour des surfaces plus exotiques.
Ok
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
