Bonsoir,
Je ne comprends absolument rien à cet exercice


. Donc si vous pourriez m'aider ce serait formidable !!! Merci d'avance.
"En première approximation, la célérité

d'une onde sonore se propageant dans l'océan varie avec la profondeur

suivant la loi :
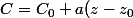^2)
,

une constante positive.
Plaçons une source sonore

immergée à la profondeur

émettant un faisceau sonore parallèle schématisé par le trajet
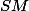
, l'inclination de l'angle
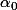
par rapport au plan horizontal. Envisageons de découper le milieu de propagation en une succession de tranches horizontales, chacune d'épaisseur infiniment petite
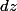
.
Compte-tenu de la symétrie du milieu, le trajet du faisceau sonore demeure dans le plan vertical
)
; il passe par le point
)
où la célérité vaut

sous l'inclination

, puis
)
où la célérité vaut
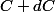
, sous l'inclination
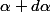
. On admettra que les ondes accoustiques suivent les mêmes lois que les ondes électromagnétiques dans le domaine du visible.
- Exprimer la pente
)
du faisceau en

puis la quantité
^2)
en fonction de l'angle

. En déduire l'équation différentielle vérifiée par la trajectoire
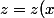)
de l'onde accoustique (il est rappelé que :
^2 = [1/cos(\alpha)^2] - 1)
).
-> pour la pente je trouve tan(\alpha) mais je suis pas sur, ensuite je vois pas comment faire !! :mur: :mur: :mur:
- L'angle \alpha est faible et la valeur
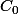
est beaucoup plus grande que celle de l'expression
^2)
. En introduisant la variable
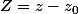
, montrer que l'équation différentielle précédente peut s'écrire sous la forme :
^2 + K_1Z^2 = K_2)
identifier les constantes
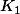
et
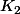
."
