[MPSI] comprends rien à cet exo d'optique
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 26 Nov 2006, 16:09
par flaja » 26 Nov 2006, 16:09
Tu as 2 équations :
 = dz/dx = z')
^2}\right) = 0)
2 inconnues :
)
et
)
(fonctions de x)
tu élimines alpha (en extrayant
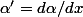
de chaque équation) et en remplaçant alpha par son expression en fonction de z' :
 = z')
Normalement, avec tous ces renseignements, tu devrais pouvoir terminer tout seul.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Nov 2006, 16:16
par pouik » 26 Nov 2006, 16:16
Donc pour la prempière equation je dois utiliser
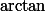
et pour la deuxième j'intègre ???
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Nov 2006, 16:45
par pouik » 26 Nov 2006, 16:45
mais le problème c'est que si je dis que :
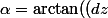/(dx)))
et en l'injectant dans la deuxième équation au bout de 4 lignes de calcul je retombe sur l'equation 2 du départ.
et je comprends pas pk ???? :mur: :mur: :mur: :mur: :mur: :mur: (oui ca m'enerve!!)
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 26 Nov 2006, 16:51
par flaja » 26 Nov 2006, 16:51
il n'y a pas à transformer tg(alpha) car les fonction de alpha peuvent s'écrire en fonction de tg(alpha) (donc z')
il n' y a rien à intégrer pour l'instant : on cherche une équa. diff.
z'' = f(z',z)
mets chacune des 2 équations sous la forme d alpha/dt = ...
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Nov 2006, 17:09
par pouik » 26 Nov 2006, 17:09
Alors là désolé mais je vois pas du tout comment faire apparaitre
)
dans les deux équations !! :doh: :doh:
Une petite piste s'il te plait.
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 26 Nov 2006, 19:17
par flaja » 26 Nov 2006, 19:17
Tu as 2 équations :
 = dz/dx = z')
^2}\right) = 0)
tu dérives la première équation par rapport à x et tu auras un d alpha/dx
dans la deuxième équation, il y a déjà un d alpha/dx quand tu développes.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Nov 2006, 19:36
par pouik » 26 Nov 2006, 19:36
oui mais pour avoir
)
dans la 1 equation il faut bien que j'écrive :
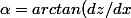)
autrement j'ai en dérivant la 1° :
(ce que j'avais mis dans mon 3ème post (celui qui étais super long).
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 26 Nov 2006, 21:19
par flaja » 26 Nov 2006, 21:19
il suffit de dériver tg(alpha) :
soit : f(alpha)
d/dx( f(alpha) ) = f '(alpha) . d alpha/dx <--- on peut exprimer d alpha/dx en fonction du reste.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 27 Nov 2006, 07:35
par pouik » 27 Nov 2006, 07:35
donc ca vaut :
^2).(d\alpha/dx))
ie
^2 + 1).(d\alpha/dx))
non ???
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 27 Nov 2006, 18:47
par flaja » 27 Nov 2006, 18:47
OUI, mais remplace dans l'équation :
 = dz/dx = z')
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 27 Nov 2006, 19:50
par pouik » 27 Nov 2006, 19:50
remplacer est-ce que ca signifie :
^2 + 1).(d\alpha/dx) = z'')
???
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 27 Nov 2006, 19:52
par pouik » 27 Nov 2006, 19:52
sinon pour l'autre equation je trouve :
)/(C_0 + a(z - z_0)^2).(d\alpha/dx) = 0)
c'est bien ca ??? :triste:
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 27 Nov 2006, 19:57
par pouik » 27 Nov 2006, 19:57
sinon est-ce que remplacer signifie remarquer que :
 = (dz/d\alpha).(d\alpha/dx))
???
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 28 Nov 2006, 22:48
par flaja » 28 Nov 2006, 22:48
remplacer est-ce que ca signifie :
^2 + 1).(d\alpha/dx) = z")
??? d
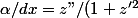)
sinon pour l'autre equation je trouve :
)/(C_0 + a(z - z_0)^2).(d\alpha/dx) = 0)
 C (d \alpha)/dx - \cos(\alpha) dC/dx)/C^2 = 0)
=>
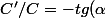 (d \alpha)/dx)
...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités