Cas d'un mouvement sans frottements

[rougedemoiselle]

Bonsoir,

Pouvez vous m'aider ?

Voici l'énoncé :
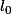
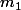
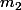
Un ressort élastique, supposé sans masse, de raideur k et de longueur au repos est placé sur un plan horizontal. Il peut-être comprimé ou allongé dans une seule direction Ox. A chacune des extrémités sont fixées des masses supposées ponctuelles,A, de masse et B de masse . Le référentiel du laboratoire est supposé galiléen.
Dans une première partie B est fixée au point 0 origine de l'axe Ox. A peut glisser sans frottements sur le plan horizontal. On repère la position de A par son abscisse . A est lâchée sans vitesse initiale à l'abscisse
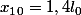
On associe au réferentiel un repère orthonormé d'origine O et tel que l'axe Oz corresponde à la verticale. Le mouvement s'effectue intégralement dans le plan horizontal et on prendra pour simplifier le ressort suivant Ox. On prendra comme origine des temps (t=0) l'instant ou on lâche A depuis l'abscisse
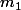
=100 g et k = 16 N.
On considère que les deux masses A et B peuvent glisser sans frottement sur le plan horizontal. Repéré par l'abscisse pour A et pour B. L'origine est prise au centre de masse G du système. Les deux masses sont lâchées sans vitesse initiale des abscisses

1/ Donner la définition du centre de masse G. Ecrire la relation entre . Quel est le mouvement de G ? Justifier la réponse.
La définition du centre de masse G je la connais. Par contre je n'arrive pas à trouver la relation. Pouvez vous m'aider ?


2/ Quel est l'allongement du ressort ? L'écrire en fonction de
Pouvez vous m'aider ?
Merci

[Dominique Lefebvre]

1/ Donner la définition du centre de masse G. Ecrire la relation entre . Quel est le mouvement de G ? Justifier la réponse.
La définition du centre de masse G je la connais. Par contre je n'arrive pas à trouver la relation. Pouvez vous m'aider ?


2/ Quel est l'allongement du ressort ? L'écrire en fonction de
Pouvez vous m'aider ?
Merci

Bonjour,
La première question est une question de cours! Il existe une relation vectorielle que tu dois connaître entre le centre de masse (ou d'inertie) G, la position des masses A et B (x1 et x2) et les masses m1 et m2 : ça a un rapport avec le barycentre...

Pour la suite, tu dois appliquer le théorème du centre de masse, qu'on appelle aussi théorème de la résultante cinétique (de mon temps), après avoir identifié les forces intérieures et extérieures de ton système. Puis un petit coup de PFD et tu pourras répondre à la question 2.

[rougedemoiselle]

Bonjour,
La première question est une question de cours! Il existe une relation vectorielle que tu dois connaître entre le centre de masse (ou d'inertie) G, la position des masses A et B (x1 et x2) et les masses m1 et m2 : ça a un rapport avec le barycentre...

Pour la suite, tu dois appliquer le théorème du centre de masse, qu'on appelle aussi théorème de la résultante cinétique (de mon temps), après avoir identifié les forces intérieures et extérieures de ton système. Puis un petit coup de PFD et tu pourras répondre à la question 2.

Donc on a pour 1/ xG = (m1 x1 + m2 x2)/(m1 + m2)
c'est ça ?

[Dominique Lefebvre]

Donc on a pour 1/ xG = (m1 x1 + m2 x2)/(m1 + m2)
c'est ça ?

On l'utilise d'habitude sous une forme plus élégante : m1*x1 + m2*x2 = 0 . Les termes en gras sont des vecteurs et x1 et x2 sont ici exprimés dans un référentiel centré sur le centre de masse.
Mais bon...
Après?

[rougedemoiselle]

On l'utilise d'habitude sous une forme plus élégante : m1*x1 + m2*x2 = 0 . Les termes en gras sont des vecteurs et x1 et x2 sont ici exprimés dans un référentiel centré sur le centre de masse.
Mais bon...
Après?

Je ne sais pas.

[Dominique Lefebvre]

Je ne sais pas.

Il faut que tu appliques le théorème du centre de masse, cela te dit quelque chose? Il te permettra d'établir l'équation recherchée...

[rougedemoiselle]

Il faut que tu appliques le théorème du centre de masse, cela te dit quelque chose? Il te permettra d'établir l'équation recherchée...

Bonsoir,

donc le centre de masse est donné par:

Si c'est cela je ne vois pas de rapport avec l'allongement mis à part que
De toute façon les masses sont toujours présentes.

[Dominique Lefebvre]

Bonjour,

J'ai un peu de temps et je viens de relire ton problème.
Dans un premier temps, la masse B est fixe et son abscisse est x2 = 0, à l'origine du repère. Seule la masse A est mobile.
On est donc dans le cas d'un oscillateur harmonique tout à fait classique (repère galiléen, pas de frottement, monodimensionnel sur l'axe Ox).
Dans ce cas, pas besoin d'utiliser le théorème du centre de masse. Il te suffit d'appliquer le PFD. Tu écartes la masse A de sa position initiale de 0,4*l0, puis tu la lâches. Sa position va osciller autour de la postion initiale x= l0. On peut calculer le mouvement en appliquant le PFD. Pendant le mouvement F = ma = -kx, que l'on peut écrire m*d²x/dt² = -k*x ou encore d²x/dt² + (k/m)*x = 0 en projetant sur Ox.
Je pense que tu sais résoudre cette équation.

J'imagine que la deuxième partie du problème consiste à libérer la masse B de telle sorte que les deux masses puissent se mouvoir.
Dans le repère choisi initalement, appliquons le théorème du centre de masse:
M*dv/dt = P1 + R1 + P2 + R2 (où M = m1+m2). Vu les hypothèses de l'énoncé, en projetant sur Ox, cette sommes est nulle, donc M*dv/dt = 0, et donc v = constante. D'après les conditions initales, la distance OG entre l'origine du repère initial et G le centre de masse est constante : le centre de masse est immobile dans notre repére.

Comme le demande ton énoncé, on centre maintenant notre référentiel sur le centre de masse G.
le théorème nous donne m1*GA + m2*GB = 0 et AB = lux . Tu dois pouvoir te débrouiller, non?
Une fois que tu l'auras résolu, on pourra trouver l'EDO du mouvement...