T60 a écrit:Bonjour,
je sais que si on lance un objet a partir de la "base" O avec un angle initial a de 45°, en negligeant tt frottements, il atteint une portee maximale, je sais aussi cmt on calcule ca.
Mais comment trouve-t-on la portee maximale avec une hauteur h initiale?
j'ai regardé ds le web et essayé un peu moi meme en mettant x(t)=v(0x)t
et en remplacant v(0x) par sina v(0) puis t par t=
[ v(0).sina +{(v(0).sina)²+2gh}^
1/2] /g
mais apres je ne sais plus continuer et sur internet on trouve souvent des resultats qui semblent differents ou du moins trouves completement differement.
Est ce que qq peut me dire cmt on fait/on continue??
Merci d'avance

T60
Deux méthodes:
- Conservation de l'énergie. Pour couper court, on pose que l'énergie est conservée (absence de frottements et/ou pertes d'énergie du a une transfo. thermique, de forme, etc...). Ainsi, a tout moment, Em = constant = Ec + Ep.
Ec peut etre trouvé, on a une formule pour Ep, on peut donc décomposer le tout en 2 dimensions et trouver la hauteur maximale du lancer. Ensuite, on en déduit le temps et/ou l'amplitude du mouvement, et on sort les propriétés d'une parabole...
-
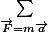
 \\<br />\vec{v}(v_x,v_y-gt) \\<br />\vec{OP}(v_x t,v_y t-g\frac{t^2}{2}))
En partant d'une vitesse constante, angle variable, on peut retrouver des cos theta et sin theta. En dérivant et trouvant le maximum de OP_x par rapport a theta, on obtient la valeur tant cherchée..
