Angle de déviation au spectroscope
De la mécanique au nucléaire, nos physiciens sont à l'écoute
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
par Kikoo <3 Bieber » 08 Sep 2012, 17:41
Salut,
J'ai un exo d'optique géométrique (dont la portée n'est que simplement calculatoire - je n'ai pour l'instant commencé aucun chapitre) :
On règle un spectroscope au minimum de déviation pour une radiation
.
On en déduit l'indice du prisme :
[CENTER]
}{\sin\(\frac{A}{2}\)})
[/CENTER]
où
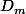
est l'angle de déviation pour une longueur d'onde
.
Sachant que
, calculer la variation
de l'angle de déviation pour une variation de la longueur d'onde
.
Je considère que chaque variation est très petite, ce qui me permet de passer par le calcul différentiel.
Tout d'abord, j'ai :
[CENTER]
}{\sin\(\frac{A}{2}\)}=a+\frac{b}{\lambda^2})
, d'où
}{\sin\(\frac{A+D_m}{2}\)-a\sin\(\frac{A}{2}\)})
[/CENTER]
Cela me fait [CENTER]
}{\sin\( \frac{A+D_m}{2}\)-a\sin\(\frac{A}{2}\)}})
[/CENTER] et je passe au logarithme :
[CENTER]
=\frac{1}{2}\ln\(\frac{b\sin\(\frac{A}{2}\)}{\sin\(\frac{A+D_m}{2}\)-a\sin\(\frac{A}{2}\)}\))
[/CENTER]
Je différencie :
[CENTER]
}{\sin\( \frac{A+D_m}{2}\)-a\sin\(\frac{A}{2}\)}\)}{\frac{b\sin\( \frac{A}{2}\)}{\sin\(\frac{A+D_m}{2}\)-a\sin\(\frac{A}{2}\)}})
[/CENTER]
Or
}{\sin\( \frac{A+D_m}{2}\)-a\sin\(\frac{A}{2}\)}\)=-\(b\sin\(\frac{A}{2}\)\)\(\frac{\cos\(\frac{A+D_m}{2}\)}{2\(\sin\(\frac{A+D_m}{2}\)-a\sin\(\frac{A}{2}\)\)^2} \)\mathrm{d} D_m)
d'où :
}{4\(\sin\(\frac{A+D_m}{2}\)-a\sin\(\frac{A}{2}\)\)}\mathrm{d} D_m)
ce qui me permet de passer à :
-a\sin\(\frac{A}{2}\)\)\mathrm{d}\lambda}{\cos\( \frac{A+D_m}{2}\)\lambda})
Le problème, c'est que ma prof a donné la solution :
[CENTER]
\mathrm{d}\lambda}{\lambda^3 \cos\( \frac{ A+D_m}{2} \)})
[/CENTER]
et je vois pas où j'ai fait des erreurs...
Merci de me les indiquer si vous les voyez
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 08 Sep 2012, 17:53
Hello,
ce que tu as fait me semble bien compliqué, pourquoi ne pas avoir dérivé directement la relation :
}{sin(\frac{A}{2})}=a+\frac{b}{\lambda ^{2}})
?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
par Kikoo <3 Bieber » 08 Sep 2012, 18:01
Hmmm... pas con :ptdr:
En différenciant de suite, j'obtiens :
}\times \frac{\cos\(\frac{A+D_m}{2}\)}{2}\mathrm{d} D_m=\frac{-2b\mathrm{d}\lambda}{\lambda^3})
d'où le résultat...
Moi= :marteau: :stupid_in :mur: ou comment chercher la complexité là où yen a pas... (mais j'ai une excuse : j'ai trop fait de calculs cette semaine !)
Merci
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
par Luc » 09 Sep 2012, 03:21
Salut,
Nightmare a raison, mais tu n'as pas fait d'erreurs de calcul. Multiplie par
pour t'en convaincre et retrouver le résultat.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
par Kikoo <3 Bieber » 09 Sep 2012, 09:58
Oui, c'est bien vrai !
Mais bon, vaut mieux que je fasse simple la prochaine fois ^^
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
par Luc » 09 Sep 2012, 12:33
Kikoo <3 Bieber a écrit:Oui, c'est bien vrai !
Mais bon, vaut mieux que je fasse simple la prochaine fois ^^
Effectivement, il vaut mieux faire un plan de calcul avant de faire des calculs, pour s'assurer que l'on fait bien exactement ce que l'on veut et pas plus.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
