Accélération , Base Fernet

[manoa]

Salut,

J'aimerais savoir comment démontrer la formule d'accélération normale sur la Base de Fernet :

[Billball]

Salut,

J'aimerais savoir comment démontrer la formule d'accélération normale sur la Base de Fernet :

ben tu as :



ensuite suffit de faire la dérivée d'un produit ..



+

et la c'est finit car

(si tu vois pas ma dernière égalité, écris

[manoa]

merci pour ta réponse :)

Mais je ne vois pas ce que signifie tau .

[Billball]

ben tau en serret frenet est définit comme :

ou encore



avec ds abscisse curviligne

[Mathusalem]

Une méthode géométrique :

Hypothèse : on possède un vecteur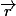 exécutant un mouvement circulaire uniforme.

La circonférence du cercle décrit par le vecteur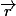 est de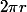

Puisque le mouvement est circulaire, il existe un vecteur constamment perpendiculaire à 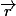, qui en est la dérivée temporelle. Par hypothèse (uniformité), le vecteur est de norme constante.
Ainsi,



est le temps que mets le vecteur vitesse à parcourir le cercle décrit par le mouvement circulaire (ou que le vecteur 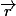met à tourner sur lui-même)

On reprend le même raisonnement pour le vecteur . Puisque le vecteur 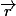est soumis à un mouvement circulaire et que le vecteur y est toujours perpendiculaire, on voit qu'en se mettant à la base du vecteur celui-ci performe également un mouvement circulaire, de circonférence .
Par les mêmes arguments, il existe alors un vecteur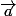 toujours perpendiculaire à et qui en est la dérivée. Ainsi, le temps que mets le vecteur à tourner sur lui même est de


Or, le temps que met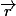 à faire un tour est identique au temps que mets à faire un tour. Ainsi, on a





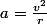
Autrement dit, on a montré qu'un mouvement circulaire uniforme implique que l'objet en mouvement (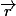) est soumis à une accélération normale de norme

EDIT: Arf, j'avais pas lu Frenet..

[manoa]

ok, mais je ne pense pas que c'est du niveau Tle , n'y aurait il pas une démo plus élémentaire ?

[Billball]

ben c'est élémentaire non? juste se servir des définitions..

[manoa]

ben c'est élémentaire non? juste se servir des définitions..

Je veux dire avec des outils niv Tle .

[Billball]

Je veux dire avec des outils niv Tle .

tout est niveau terminal non?? désolé, je connais pas d'autre méthode sinon :triste:

[manoa]

tout est niveau terminal non?? désolé, je connais pas d'autre méthode sinon :triste:

On a quasiment fini la méca , et sur la base de Frenet on n'a vu que ces deux relations tombées du ciel :
, c'est pas grave sino je vais chercher à comprendre ce que tu m'a donné déjà , merci !

@Mathusalem : merci , je vais vérifier ça

[Billball]

On a quasiment fini la méca , et sur la base de Frenet on n'a vu que ces deux relations tombées du ciel :
, c'est pas grave sino je vais chercher à comprendre ce que tu m'a donné déjà , merci !

@Mathusalem : merci , je vais vérifier ça

et bah c'est ce que je t'ai démontré au dessus alors!

si t'as des qtions hésite pas..