Vrai ...ou faux LES SUITES....!!
15 messages
- Page 1 sur 1
vrai ...ou faux LES SUITES....!!
Bonsoir
a)si (Un) converge,alors (U²n) converge.
b)si (U²n) converge alors converge
c)si (Un)est bornée , alors (Un) converge
d)si (Un) converge,alors (Un) est bornée
e) si (U²n) est bornée, alors (Un) est bornée
mais réponses : a) vrai ;b)faux ;c)faux ;d) je sais pas ;e) je sais pas
aidez moi s'il vous plait et dites moi si ce que j'ai fais est bon oi po ...
et merci d'avance
a)si (Un) converge,alors (U²n) converge.
b)si (U²n) converge alors converge
c)si (Un)est bornée , alors (Un) converge
d)si (Un) converge,alors (Un) est bornée
e) si (U²n) est bornée, alors (Un) est bornée
mais réponses : a) vrai ;b)faux ;c)faux ;d) je sais pas ;e) je sais pas
aidez moi s'il vous plait et dites moi si ce que j'ai fais est bon oi po ...
et merci d'avance
mostdu95 a écrit:d'accord mais il y'a un problème pour la b car moi aussi j'ai posé Un= (-1)^n
et dc (U²n)= (-1)^2n = 1^n
la raison est egale à 1 donc c'est une suite stationnaire donc elle ne converge pas
Si une suite qui donne systématiquement la même valeur ne converge pas, peux tu me donner une suite qui converge ?
1^n ne convergerait elle pas vers 1 par hasard ?
Bonjour
la 1. Il faut revenir à la définition de la limite ce n'est pas bien dûr
Pour tout epsilon fixé , A partir d'un certain rang N,
Alors
D'où :
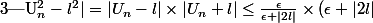=\epsilon) CQFD
CQFD
La 2.
A partir d'un certain rang N,
Donc (Un) est bornée pour n > N
Pour n inférieur à N il y a un nombre fini de termes. On considère M le plus grand et m le plus petit.
Alors (Un) est clairement majoré par) et minoré par
et minoré par )
5. Je l'ai démontrée.
la 1. Il faut revenir à la définition de la limite ce n'est pas bien dûr
Pour tout epsilon fixé , A partir d'un certain rang N,
Alors
D'où :
La 2.
A partir d'un certain rang N,
Donc (Un) est bornée pour n > N
Pour n inférieur à N il y a un nombre fini de termes. On considère M le plus grand et m le plus petit.
Alors (Un) est clairement majoré par
5. Je l'ai démontrée.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
