Bonjour,
J'ai essayé de démontrer la formule du volume d'un cône mais je ne retombe pas sur le bon resultat: voici ma demonstration.
On se place dans un repère (O;x,y,z).
On place les points H,R et O de coordonnees respectivement (h,0,0) ; (0,r,0) ; (0,0,0) avec h hauteur du cône et r son rayon à la base.
On découpe le cône verticalement en un point x(x,0,0). On obtient alors un rayon variable r(x).
Dans le triangle HOR rectangle en O, on note A le point d'intersection entre le cercle de centre x et de rayon r(x) et le segment HR.
D'une part , x appartient à [HO] et A appartient à [HR]
D'autre (xA) est parallele à (OR)
Par le théorème de Thalès , (h-x)/h = r(x) / r soit r(x) =[ (h-x)/h ] *r
Le volume du cylindre de rayon r(x) et de hauteur infinitésimal dx est V(x)= pi*[( r^2 / h)*x^2 + r^2]dx
Puis j'integre ce volume de 0 à h et je trouve V(cône ) = 4/3 * pi * r^2 * h
Trouvez vous une erreur ?
Merci
Volume du cône
8 messages
- Page 1 sur 1
Re: Volume du cône
Bonjour
Je ne sais ce que tu as fait mais avec Thalès on a !!!
!!!
dc=hR/H)
Si tu intègres :^2 dh) ça doit être bon.
ça doit être bon.
Je ne sais ce que tu as fait mais avec Thalès on a
dc
Si tu intègres :
Re: Volume du cône
Dans ce que j'ai posé: H n'est pas une distance c'est un point d'abscisse h avec h qui représente la hauteur du cône. Donc h ne varie pas.
Re: Volume du cône
De toute façon ton application de Thalès et la suite est bien difficile à comprendre (on est perdu avec r(x) et r et avec tes notations.)
Pour pouvoir dire où il y a erreur il faudrait clarifier tes notations.
Pour pouvoir dire où il y a erreur il faudrait clarifier tes notations.
Re: Volume du cône
Je vais redéfinir certains objets.
Soit x le point de coordonnées (x,0,0).
On considère le cercle de centre x tel que le plan dans lequel est contenu ce cercle est parallèle au plan (0yz).
r(x) est le rayon du cercle de centre x.
Voici une représentation 3D et une représentation dans le plan de la situation.


Enfin, je détaille le passage du théorème de Thalès:
D'une part et
et  .
.
D'autre part \parallel (OR)) .
.
Alors, par le théorème de Thalès appliqué au triangle OHR rectangle en O , on a:
}{r}} \leftrightarrow {r(x)=\frac{h-x}{h} r) .
.
Soit x le point de coordonnées (x,0,0).
On considère le cercle de centre x tel que le plan dans lequel est contenu ce cercle est parallèle au plan (0yz).
r(x) est le rayon du cercle de centre x.
Voici une représentation 3D et une représentation dans le plan de la situation.


Enfin, je détaille le passage du théorème de Thalès:
D'une part
D'autre part
Alors, par le théorème de Thalès appliqué au triangle OHR rectangle en O , on a:
Re: Volume du cône
Salut,\!=\!\dfrac{h\!-\!x}h r) à ton
à ton ) .
.
Le volume du cylindre, c'est la surface du disque de rayon) donc
donc \big)^{\!2}) multiplié par la hauteur
multiplié par la hauteur 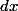 :
:
=\pi\Big(\dfrac{h-x}{h}r\Big)^{\!2}dx<br />=\pi\Big(r-\dfrac{r}{h}x\Big)^{\!2}dx<br />=\pi\Big(r^2-2r\dfrac{r}{h}x+\big(\dfrac{r}{h}x\big)^{\!2}\Big)dx<br />=\pi\Big(r^2-\dfrac{2r^2}{h}x+\dfrac{r^2}{h^2}x^2\Big)dx)
Ce qui n'a franchement rien à voir avec ton=\pi\Big(\dfrac{r^2}{h}x^2\!+\!r^2\Big)dx) qui est clairement absurde vu qu'il ne donne pas 0 lorsque
qui est clairement absurde vu qu'il ne donne pas 0 lorsque  (c'est pas con de faire un dessin, mais c'est encore moins con de s'en servir pour vérifier qu'on a pas écrit des énormités...)
(c'est pas con de faire un dessin, mais c'est encore moins con de s'en servir pour vérifier qu'on a pas écrit des énormités...)
Sans parler du fait que pour intégrer de 0 à la quantité
la quantité ) , c'est vraiment pas malin de développer : une primitive de
, c'est vraiment pas malin de développer : une primitive de ^2) , c'est bien évidement
, c'est bien évidement ^3) .
.
Je comprend pas comment tu passe de tonmaths920 a écrit:. . .soit r(x) =[ (h-x)/h ] *r
Le volume du cylindre de rayon r(x) et de hauteur infinitésimal dx est V(x)= pi*[( r^2 / h)*x^2 + r^2]dx . . .
Le volume du cylindre, c'est la surface du disque de rayon
Ce qui n'a franchement rien à voir avec ton
Sans parler du fait que pour intégrer de 0 à
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Volume du cône
C'est bon, je sais d'où vient mon erreur, merci!
J'ai fait ceci:
=\frac{h-x}{h}r = (1- \frac{x}{h})r = r - \frac{x}{h} r)
Puis, au lieu d'élever la parenthèse au carré dans la formule du volume du cylindre, j'ai élevé chaque membre de) au carré.
au carré.
J'ai fait ceci:
Puis, au lieu d'élever la parenthèse au carré dans la formule du volume du cylindre, j'ai élevé chaque membre de
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
